题目内容
11.已知动点P(x,y)在椭圆C:$\frac{x^2}{25}+\frac{y^2}{16}$=1上,F为椭圆C的右焦点,若点M满足|$\overrightarrow{MF}$|=1且$\overrightarrow{PM}•\overrightarrow{MF}$=0,则|$\overrightarrow{PM}$|的最小值为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{12}{5}$ | D. | 1 |
分析 依题意知,该椭圆的焦点F(3,0),点M在以F(3,0)为圆心,1为半径的圆上,当PF最小时,切线长PM最小,作出图形,即可得到答案.
解答 解:依题意知,点M在以F(3,0)为圆心,1为半径的圆上,PM为圆的切线,
且$\overrightarrow{PM}•\overrightarrow{MF}$=0,即PM⊥MF,
∴|PM|2=|PF|2-|MF|2,而|MF|=1,
∴当PF最小时,切线长PM最小.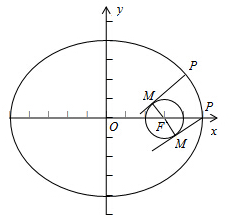
由图知,当点P为右顶点(5,0)时,|PF|最小,最小值为:5-3=2.
此时|PM|=$\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
故选:A.
点评 本题考查椭圆的标准方程、圆的方程,考查作图与分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.“a=10“是“直线ax+4y-2=0与2x-5y+b=0互相垂直”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也必要条件 |
2.若圆心为(3,1)的圆与x轴相切,则该圆的方程是( )
| A. | x2+y2-2x-6y+9=0 | B. | x2+y2+6x+2y+9=0 | C. | x2+y2-6x-2y+9=0 | D. | x2+y2+2x+6y+9=0 |
6.已知集合A={x|y=$\sqrt{x(x-1)}$+$\sqrt{x}$},集合B={y|y=sinx+$\sqrt{3}$cosx,x∈R},全集为R,则(∁RA)∩B为( )
| A. | [-2,2) | B. | [-2,1) | C. | [-2,0)∪(0,1) | D. | [-2,0)∪(0,2] |
16.函数f(x)=3sin2x+2sinxcosx+cos2x-2的单调递减区间是( )
| A. | $[kπ+\frac{3π}{8},kπ+\frac{7π}{8}],k∈Z$ | B. | $[2kπ+\frac{3π}{8},2kπ+\frac{7π}{8}],k∈Z$ | ||
| C. | $[2kπ-\frac{π}{8},2kπ+\frac{3π}{8}],k∈Z$ | D. | $[kπ-\frac{π}{8},kπ+\frac{3π}{8}],k∈Z$ |