题目内容
曲线y=x2与其在x=±1处的切线所围成的图形的面积是 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：根据导数的几何意义求出切线方程，作出对应的图象，利用积分的几何意义即可求区域面积．
解答：
解：曲线y=f（x）=x2的导数f′（x）=2x，
则f′（1）=2，f′（-1）=-2，
则函数在x=1处的切点为（1，1），切线斜率k=f′（1）=2，则对应的切线方程为y-1=2（x-1），即y=2x-1，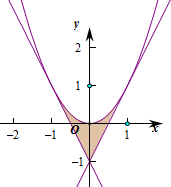
函数在x=-1处的切点为（-1，1），切线斜率k=f′（-1）=-2，则对应的切线方程为y-1=-2（x+1），即y=-2x-1，
作出对应的图象为（阴影部分）：
则由积分以及函数的对称性可知，所围成的图形的面积S=2
[x2-(2x-1)]dx=2[（
x3-x2+x）|
]=2×（
-1+1）=
，
故答案为：
则f′（1）=2，f′（-1）=-2，
则函数在x=1处的切点为（1，1），切线斜率k=f′（1）=2，则对应的切线方程为y-1=2（x-1），即y=2x-1，
函数在x=-1处的切点为（-1，1），切线斜率k=f′（-1）=-2，则对应的切线方程为y-1=-2（x+1），即y=-2x-1，
作出对应的图象为（阴影部分）：
则由积分以及函数的对称性可知，所围成的图形的面积S=2
| ∫ | 1 0 |
| 1 |
| 3 |
1 0 |
| 1 |
| 3 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题主要考查导数的几何意义以及积分的应用，要求熟练掌握相应的导数公式以及积分公式．
练习册系列答案
备战中考寒假系列答案
相关题目
某几何体的三视图如图所示，主视图和左视图是长为3，宽为2的矩形，俯视图是边长为2的正方形，则该几何体的体积为
如图所示阴影部分由3个小方格组成，我们称这样的图形为L形（每次旋转90°仍为L形），那么在由4×5个小方格构成的方格纸上任取三个小方格，这三个小方格恰好能构成L形的概率是