题目内容
已知sin(x+
)=
,则sin(
-x)+sin2(
-x)的值为 .
| π |
| 6 |
| 1 |
| 4 |
| 5π |
| 6 |
| π |
| 3 |
考点:二倍角的余弦,两角和与差的正弦函数
专题:三角函数的求值
分析:由已知中sin(x+
)=
,利用诱导公式和同角三角函数的基本关系公式,可得sin(
-x)=
,sin2(
-x)=cos2(x+
)=1-sin2(x+
),代入可得答案.
| π |
| 6 |
| 1 |
| 4 |
| 5π |
| 6 |
| 1 |
| 4 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
解答:
解:∵sin(x+
)=
,
∴sin(
-x)=sin[π-(x+
)]=sin(x+
)=
,
sin2(
-x)=sin2[
-(x+
)]=cos2(x+
)=1-sin2(x+
)=
,
∴sin(
-x)+sin2(
-x)=
+
=
,
故答案为:
| π |
| 6 |
| 1 |
| 4 |
∴sin(
| 5π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 4 |
sin2(
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 15 |
| 16 |
∴sin(
| 5π |
| 6 |
| π |
| 3 |
| 1 |
| 4 |
| 15 |
| 16 |
| 19 |
| 16 |
故答案为:
| 19 |
| 16 |
点评:本题考查的知识是诱导公式和同角三角函数的基本关系公式,其中分析出已知角和未知角的关系,进而选择恰当的公式,是解答的关键.

练习册系列答案
相关题目
不等式log3|x-
|<-1的解集是( )
| 1 |
| 3 |
A、(0,
| ||||||
B、(
| ||||||
C、(0,
| ||||||
D、(
|
设函数y=f(x),x∈[a,b],其导函数的图象如图所示,则函数y=f(x)的减区间是( )
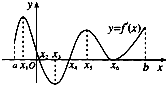

| A、(x1,x3) |
| B、(x2,x4) |
| C、(x4,x6) |
| D、(x5,x6) |
设Sn为等差数列{an}的前n项和,(n+1)Sn<nSn+1(n∈N*).若
<-1,则( )
| a8 |
| a7 |
| A、Sn的最大值为S8 |
| B、Sn的最小值为S8 |
| C、Sn的最大值为S7 |
| D、Sn的最小值为S7 |