题目内容
19.函数f(x)=sin2x和函数g(x)的部分图象如图所示,则函数g(x)的解析式可以是( )
| A. | g(x)=sin(2x-$\frac{π}{3}}$) | B. | g(x)=sin(2x+$\frac{2π}{3}}$) | C. | g(x)=cos(2x+$\frac{5π}{6}}$) | D. | g(x)=cos(2x-$\frac{π}{6}}$) |
分析 由图象可得g(x)的图象经过点($\frac{17π}{24}$,$\frac{\sqrt{2}}{2}$),逐个选项验证可得.
解答 解:代值计算可得f($\frac{π}{8}$)=sin$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
由图象可得g(x)的图象经过点($\frac{17π}{24}$,$\frac{\sqrt{2}}{2}$),
代入验证可得选项A,g($\frac{17π}{24}$)=sin$\frac{13π}{12}$≠$\frac{\sqrt{2}}{2}$,故错误;
选项B,g($\frac{17π}{24}$)=sin$\frac{25π}{12}$≠$\frac{\sqrt{2}}{2}$,故错误;
选项D,g($\frac{17π}{24}$)=cos$\frac{15π}{12}$=-cos$\frac{π}{4}$=≠$\frac{\sqrt{2}}{2}$,故错误;
选项C,g($\frac{17π}{24}$)=cos$\frac{27π}{12}$=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,故正确.
故选:C.
点评 本题考查三角函数图象和解析式,逐个验证是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.若集合$A=\{x|\frac{x+5}{x-2}<0\}$,B={x|-4<x<3},则集合A∩B为( )
| A. | {x|-5<x<3} | B. | {x|-4<x<2} | C. | {x|-4<x<5} | D. | {x|-2<x<3} |
14.已知集合A={x|x2+2x-8≥0},B={x|1<x<5},U=R,则CU(A∪B)( )
| A. | (-4,1] | B. | [-4,1) | C. | (-2,1] | D. | [-2,1) |
11.执行如图所示的程序框图,输出的i为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
9.过曲线y=$\frac{1}{8}$x4上一点P(2,2)的切线的斜率是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
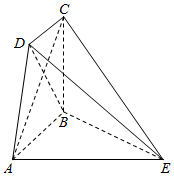 如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.
如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.