题目内容

4．直线x=1，x=2，y=0及曲线y=x3围成的平面图形的面积为（　　）
A．$\sum_{i=1}^{n}$$\frac{1}{n}$（1+$\frac{i}{n}$）3B．${∫}_{1}^{2}$x3dxC．${∫}_{2}^{1}$x3dxD．1

分析 利用定积分表示区域面积，即可得出结论．

解答 解：由题意，直线x=1，x=2，y=0及曲线y=x3围成的平面图形的面积为S=${∫}_{1}^{2}$x3dx，
故选：B．

点评 本小题考查根据定积分的几何意义，以及会利用定积分求图形面积的能力，属于基础题．

练习册系列答案
相关题目
14．已知集合A={x|x2+2x-8≥0}，B={x|1＜x＜5}，U=R，则CU（A∪B）（　　）
A．（-4，1]B．[-4，1）C．（-2，1]D．[-2，1）
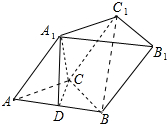15．已知抛物线C1：y2=16x上的点P到圆C2：（x-4）2+y2=$\frac{32}{41}$的圆心的距离等于8，则抛物线C1在点P处的切线l1与C2经过点P的切线l2构成的角中，较小的角θ的正切值等于$\frac{4}{5}$．
12．如图，三棱柱ABC-A1B1C1中，A1C⊥底面ABC，∠ACB=120°，A1C=AC=BC=2，D为AB中点．
（1）求证：平面A1CD⊥平面A1AB；
（2）求二面角A1-BC-C1的余弦值．
19．已知sin22α+sin2αcosα-cos2α=1，求锐角α．
9．过曲线y=$\frac{1}{8}$x4上一点P（2，2）的切线的斜率是（　　）
A．1B．2C．4D．8
16．直线l经过两直线l1：2x-3y+8=0，l2：3x+4y-5=0的交点A．
（1）求与直线3x-2y+4=0平行的直线l的方程；
（2）若原点O到直线l距离等于1，求直线l的方程．
13．$\overrightarrow{a}•\overrightarrow{b}$=6，|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2$\sqrt{2}$，则，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=45°．
14．求下列函数的导数：
（1）y=（2x2+3x+1）5；
（2）y=esinx；
（3）y=tan$\frac{1}{x}$；
（4）y=$\sqrt{1-{x}^{2}}$；
（5）y=ln（lnx）；
（6）y=cos（2x+$\frac{π}{6}$）；
（7）y=ln$\frac{x-1}{x+1}$；
（8）y=2xcos3x；
（9）y=x2lnx．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网