题目内容
2.某研究性学习小组为了解学生每周用于体育锻炼时间的情况,在甲、乙两所学校随机抽取了各50名学生,做问卷调查,并作出如下频率分布直方图: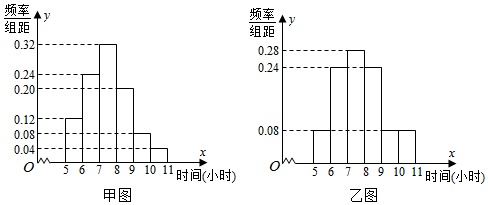
(Ⅰ)根据直方图计算:两所学校被抽取到的学生每周用于体育锻炼时间的平均数;
(Ⅱ)在这100名学生中,要从每周用于体育锻炼时间不低于10小时的学生中选出3人,该3人中来自乙学校的学生数记为X,求X的分布列和数学期望.
分析 (Ⅰ)由频率分布直方图能求出两所学校被抽取到的学生每周用于体育锻炼时间的平均数.
(Ⅱ)每周体育锻炼时间不低于10个小时的学生中,甲校有2人,乙校有4人,X的所有可能取值有1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由频率分布直方图得甲校被抽取到的学生每周用于体育锻炼时间的平均数为:
$\overline{{x}_{甲}}$=0.12×5.5+0.24×6.5+0.32×7.5+0.20×8.5+0.08×9.5+0.04×10.5=7.5.
乙校被抽取到的学生每周用于体育锻炼时间的平均数为:
$\overline{{x}_{乙}}$=0.08×5.5+0.24×6.5+0.28×7.5+0.24×8.5+0.08×9.5+0.08×10.5=7.74.
(Ⅱ)每周体育锻炼时间不低于10个小时的学生中,甲校有2人,乙校有4人,
X的所有可能取值有1,2,3,
P(X=1)=$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(X=2)=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(X=3)=$\frac{{C}_{2}^{0}{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查平均数的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图的性质的合理运用.

练习册系列答案
相关题目
12.函数f(x)=cosx•log2|x|的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
13.已知i是虚数单位,则复数z=$\frac{1+2i}{3-4i}$的虚部是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{2}{5}$i |
17.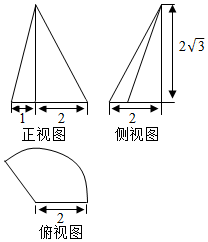 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )| A. | 4+$\frac{4π}{3}$ | B. | 6$\sqrt{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 6 |
7.若集合$A=\{x|\frac{x+5}{x-2}<0\}$,B={x|-4<x<3},则集合A∩B为( )
| A. | {x|-5<x<3} | B. | {x|-4<x<2} | C. | {x|-4<x<5} | D. | {x|-2<x<3} |
14.已知集合A={x|x2+2x-8≥0},B={x|1<x<5},U=R,则CU(A∪B)( )
| A. | (-4,1] | B. | [-4,1) | C. | (-2,1] | D. | [-2,1) |
11.执行如图所示的程序框图,输出的i为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
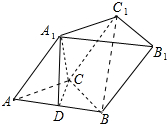 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.