题目内容
6．已知命题p：?x∈R，|1-x|-|x-5|＜a，若?p为假命题，则a的取值范围是（4，+∞）．分析 利用全称命题的否定是特称命题，判断全称命题是真命题，求解即可．
解答 解：命题p：?x∈R，|1-x|-|x-5|＜a，若?p为假命题，可知全称命题是真命题，即：?x∈R，|1-x|-|x-5|＜a恒成立，因为，|1-x|-|x-5|≤4，所以a＞4．
则a的取值范围是（4，+∞）．
故答案为：（4，+∞）．
点评 本题考查命题的否定，特称命题与全称命题的否定关系，函数恒成立条件的应用，是基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
16．若函数f（x）=$\left\{\begin{array}{l}{lnx，（x＞0）}\\{{e}^{x+1}-2，（x≤0）}\end{array}\right.$，则f（f（$\frac{1}{e}$））=（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 3 |
17．
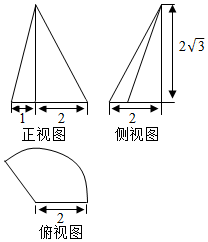某几何体的三视图如图所示，其中俯视图为扇形，则一个质点从扇形的圆心起始，绕几何体的侧面运动一周回到起点，其最短路径为（ ）
某几何体的三视图如图所示，其中俯视图为扇形，则一个质点从扇形的圆心起始，绕几何体的侧面运动一周回到起点，其最短路径为（ ）| A． | 4+$\frac{4π}{3}$ | B． | 6$\sqrt{3}$ | C． | 4+$\frac{2π}{3}$ | D． | 6 |
14．已知集合A={x|x2+2x-8≥0}，B={x|1＜x＜5}，U=R，则CU（A∪B）（ ）
| A． | （-4，1] | B． | [-4，1） | C． | （-2，1] | D． | [-2，1） |
1．已知点列${A_n}（{{a_n}，{b_n}}）（{n∈{N^*}}）$是函数y=ax（a＞0，a≠1）图象上的点，点列Bn（n，0）满足|AnBn|=|AnBn+1|，若数列{bn}中任意相邻三项能构成三角形三边，则a的取值范围是（ ）
| A． | $0＜a＜\frac{{\sqrt{5}-1}}{2}$或$a＞\frac{{\sqrt{5}+1}}{2}$ | B． | $\frac{{\sqrt{5}-1}}{2}＜a＜1$或$1＜a＜\frac{{\sqrt{5}+1}}{2}$ | ||
| C． | $0＜a＜\frac{{\sqrt{3}-1}}{2}$或$a＞\frac{{\sqrt{3}+1}}{2}$ | D． | $\frac{{\sqrt{3}-1}}{2}＜a＜1$或$1＜a＜\frac{{\sqrt{3}+1}}{2}$ |
11．执行如图所示的程序框图，输出的i为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |