题目内容
14. 在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.
在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.
分析 根据几何概型的概率公式求出对应区域的面积进行计算即可.
解答 解:设圆的比较为R,则正方形的边长为2R,
则阴影部分的面积S=$\frac{1}{4}×π×{R}^{2}$=$\frac{π{R}^{2}}{4}$,
则对应概率P=$\frac{\frac{π{R}^{2}}{4}}{2R•2R}$=$\frac{π}{16}$,
故答案为:$\frac{π}{16}$.
点评 本题主要考查几何概型的概率的计算,求出对应区域的面积是解决本题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.函数f(x)=$\left\{\begin{array}{l}\frac{1}{2^x},x≤0\\ 2sin(2x+\frac{π}{6}),0<x<π\end{array}$若x1,x2,x3是方程f(x)+a=0三个不同的根,则x1+x2+x3的范围是( )
| A. | $(-1,\frac{π}{2})$ | B. | $(\frac{π}{3}-1,\frac{π}{3})$ | C. | $(\frac{π}{3}-1,\frac{π}{3}+1)$ | D. | $(\frac{π}{6},\frac{π}{6}+1)$ |
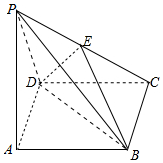 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点.