题目内容
5.直三棱柱ABC-A1B1C1中,AB=AC=2,$∠BAC=\frac{2π}{3}$,AA1=4,则该三棱柱的外接球的体积为$\frac{{64\sqrt{2}π}}{3}$.分析 由题意可知直三棱柱ABC-A1B1C1中,AB=AC=2,$∠BAC=\frac{2π}{3}$,AA1=4,底面ABC的小圆半径为2,连接两个底面中心的连线,中点与顶点的连线就是球的半径,即可求出三棱柱的外接球的体积.
解答 解:由题意可知直三棱柱ABC-A1B1C1中,AB=AC=2,$∠BAC=\frac{2π}{3}$,AA1=4,底面小圆ABC的半径为2,连接两个底面中心的连线,中点与顶点的连线就是球的半径,外接球的半径为:$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴三棱柱的外接球的体积为$\frac{{64\sqrt{2}π}}{3}$
故答案为:$\frac{{64\sqrt{2}π}}{3}$.
点评 本题是中档题,考查直三棱柱的外接球的体积的求法,解题的关键是外接球的半径,直三棱柱的底面中心的连线的中点与顶点的连线是半径,考查空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若a、b都是正数,则关于x的不等式$-b<\frac{1}{x}<a$的解集是( )
| A. | $(-\frac{1}{b},0)∪(0,\frac{1}{a})$ | B. | $(-\frac{1}{a},0)∪(0,\frac{1}{b})$ | C. | $(-∞,-\frac{1}{b})∪(\frac{1}{a},+∞)$ | D. | $(-\frac{1}{a},\frac{1}{b})$ |
17.已知f(x)是定义在R上的偶函数,且f(2)=8,则f(-2)的值为( )
| A. | -16 | B. | 16 | C. | -8 | D. | 8 |
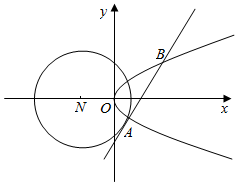 如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B. 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AB∥DC,∠ABC=∠CAD=90°,且PA=AB=BC=1,E是棱PB上的点,且PE=2EB. 在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.
在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系. 在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.
在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.