题目内容
19.函数f(x)=$\left\{\begin{array}{l}\frac{1}{2^x},x≤0\\ 2sin(2x+\frac{π}{6}),0<x<π\end{array}$若x1,x2,x3是方程f(x)+a=0三个不同的根,则x1+x2+x3的范围是( )| A. | $(-1,\frac{π}{2})$ | B. | $(\frac{π}{3}-1,\frac{π}{3})$ | C. | $(\frac{π}{3}-1,\frac{π}{3}+1)$ | D. | $(\frac{π}{6},\frac{π}{6}+1)$ |
分析 作函数f(x)=$\left\{\begin{array}{l}\frac{1}{2^x},x≤0\\ 2sin(2x+\frac{π}{6}),0<x<π\end{array}$的图象,从而可得-2<a<-1,从而结合图象解得.
解答 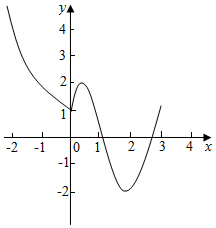 解:作函数f(x)=$\left\{\begin{array}{l}\frac{1}{2^x},x≤0\\ 2sin(2x+\frac{π}{6}),0<x<π\end{array}$的图象如下,
解:作函数f(x)=$\left\{\begin{array}{l}\frac{1}{2^x},x≤0\\ 2sin(2x+\frac{π}{6}),0<x<π\end{array}$的图象如下,
∵x1,x2,x3是方程f(x)+a=0三个不同的根,
∴方程f(x)=-a有三个不同的根,
∴1<-a<2,∴-2<a<-1;
不妨设x1<x2<x3,
∵sin(2x+$\frac{π}{6}$)=1,∴x=$\frac{π}{6}$;
结合图象可知,
x2+x3=$\frac{π}{6}$×2=$\frac{π}{3}$;
∵1<2-x<2,
∴-1<x<0,
∴-1<x1<0,
∴x1+x2+x3∈$(\frac{π}{3}-1,\frac{π}{3})$.
故选:B.
点评 本题考查了方程的根与函数的图象的关系应用及数形结合的思想应用.

练习册系列答案
相关题目
9.执行如图所示的程序框图,则输出S的值为( )


| A. | -10 | B. | 6 | C. | 8 | D. | 14 |
11.下列各角中,与60°角终边相同的角是( )
| A. | -60° | B. | 600° | C. | 1020° | D. | -660° |
8.已知三棱柱ABC-A1B1C1的侧棱和底面垂直,底面是正三角形,侧棱长是底边长的2倍,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为36π,则此三棱锥A-A1B1C1的体积为( )
| A. | $\frac{121}{25}$ | B. | $\frac{81}{16}$ | C. | $\frac{16}{9}$ | D. | $\frac{9}{4}$ |
 在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.
在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.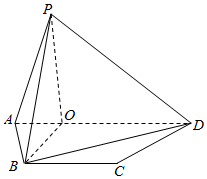 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2. 在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.
在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.