题目内容
4.计算下列各题:(1)${(0.027)^{-\frac{1}{3}}}-{(-\frac{1}{7})^{-2}}+{(2\frac{7}{9})^{\frac{1}{2}}}-{(\sqrt{2}-1)^0}$
(2)${log_5}35+2{log_{\frac{1}{2}}}\sqrt{2}-{log_5}\frac{1}{50}-{log_5}14+{5^{{{log}_5}3}}$.
分析 利用有理数指数幂和对运算法则计算.
解答 解:(1)原式=(0.33)${\;}^{-\frac{1}{3}}$-(7-1)-2+[($\frac{5}{3}$)2]${\;}^{\frac{1}{2}}$-1=0.3-1-72+$\frac{5}{3}$-1=$\frac{10}{3}$-49+$\frac{5}{3}$-1=-45.
(2)原式=log535+log550-log514+log${\;}_{\frac{1}{2}}$2+3=log5($\frac{35×50}{14}$)-1+3=log5125+2=3+2=5.
点评 本题考查了对数运算法则,有理数指数幂运算,属于基础题.

练习册系列答案
相关题目
14.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下:f(1)=-2,f(1.5)=0.625;f(1.25)=-0.984,f(1.375)=-0.260;
f(1.438)=0.165,f(1.4065)=-0.052.
那么方程x3+x2-2x-2=0的一个近似根可以为(精确度为0.1)( )
f(1.438)=0.165,f(1.4065)=-0.052.
那么方程x3+x2-2x-2=0的一个近似根可以为(精确度为0.1)( )
| A. | 1.2 | B. | 1.35 | C. | 1.43 | D. | 1.5 |
15.若a、b都是正数,则关于x的不等式$-b<\frac{1}{x}<a$的解集是( )
| A. | $(-\frac{1}{b},0)∪(0,\frac{1}{a})$ | B. | $(-\frac{1}{a},0)∪(0,\frac{1}{b})$ | C. | $(-∞,-\frac{1}{b})∪(\frac{1}{a},+∞)$ | D. | $(-\frac{1}{a},\frac{1}{b})$ |
9.执行如图所示的程序框图,则输出S的值为( )


| A. | -10 | B. | 6 | C. | 8 | D. | 14 |
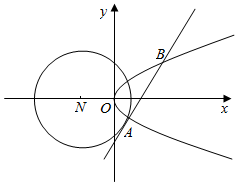 如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B.
如图所示:已知圆N:(x+2)2+y2=8和抛物线C:y2=2x,圆N的切线l与抛物线C交于不同的两点A,B. 在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.
在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.