题目内容
2.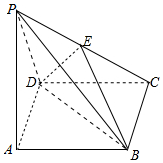 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,PD⊥CD,E为PC的中点.(Ⅰ)求证:平面ABE⊥平面PCD;
(Ⅱ)求二面角B-DE-C的余弦值.
分析 (Ⅰ)根据面面垂直的判定定理进行证明即可.
(2)建立空间直角坐标系,利用向量法进行求解即可.
解答  解:(Ⅰ)取PD的中点F,连接AF,EF,
解:(Ⅰ)取PD的中点F,连接AF,EF,
∵△PAD为正三角形,∴AF⊥PD,
∵AD⊥CD,PD⊥CD,AD∩PD=D,
∴CD⊥平面PAD,
∵AF?平面PAD,∴CD⊥AF,
∵CD∩PD=D,∴AF⊥平面PCD,
∵E为PC的中点,∴EF∥CD,
∵AB∥CD,∴AB∥EF,
∵AF?平面ABE,∴平面ABE⊥平面PCD;
(Ⅱ)取AD,BC的中点O,M,连接PO,OM,
∴OM⊥AD,
∵PA=PD,∴PO⊥AD,
∵CD⊥平面PAD,PO?平面PAD,
∴CD⊥PO,
∵OM∥CD,∴OM⊥PO,
以O为坐标原点,分别以OA,OM,OP,为x,y,z轴建立空间直角坐标系如图:
设AD=1,则D(0,0,0),A($\frac{1}{2}$,0,0),B($\frac{1}{2}$,1,0),C(-$\frac{1}{2}$,1,0),D(-$\frac{1}{2}$,0,0),P(0,0,$\frac{\sqrt{3}}{2}$),E(-$\frac{1}{4}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),F(-$\frac{1}{4}$,0,$\frac{\sqrt{3}}{4}$),
则$\overrightarrow{AF}$=(-$\frac{3}{4}$,0,$\frac{\sqrt{3}}{4}$),
∵AF⊥平面PCD,
∴平面CDE的一个法向量为$\overrightarrow{m}$=($\sqrt{3}$,0,-1),
设平面BDE的法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{BD}$=(-1,-1,0),$\overrightarrow{DE}$=($\frac{1}{4}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),
则由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BD}=0}\\{\overrightarrow{n}•\overrightarrow{DE}=0}\end{array}\right.$得$\left\{\begin{array}{l}{-x-y=0}\\{\frac{1}{4}x+\frac{1}{2}y+\frac{\sqrt{3}}{4}z=0}\end{array}\right.$,
可取$\overrightarrow{n}$=(1,-1,$\frac{\sqrt{3}}{3}$),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{{\sqrt{7}}}{7}$.
即二面角B-DE-C的余弦值是$\frac{{\sqrt{7}}}{7}$.
点评 本题综合考查空间中面面垂直的判断和空间角的计算,涉及二面角的平面角,利用向量法是解决空间角常用的方法,考查的知识面较广,综合性较强,运算量较大.

| A. | -16 | B. | 16 | C. | -8 | D. | 8 |
| A. | -60° | B. | 600° | C. | 1020° | D. | -660° |
 在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.
在空中,取直线l为轴,直线l与l′相交于O点,夹角为30°,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面.已知直线l∥平面α,l与α的距离为2,平面α与圆锥面相交得到双曲线Γ.在平面α内,以双曲线Γ的中心为原点,以双曲线的两个焦点所在直线为y轴,建立直角坐标系.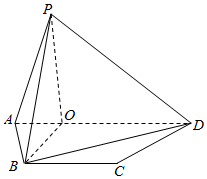 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2. 在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.
在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率是$\frac{π}{16}$.