题目内容
 如图,四棱锥S-ABCD中,△SAB是正三角形,四边形ABCD为正方形,平面SAB⊥平面ABCD,AB=BC=4,E为SB中点,点F在线段BC上.
如图,四棱锥S-ABCD中,△SAB是正三角形,四边形ABCD为正方形,平面SAB⊥平面ABCD,AB=BC=4,E为SB中点,点F在线段BC上.(Ⅰ)当EF⊥BD时,求BF的长度;
(Ⅱ)设二面角E-AF-B的大小为θ,当点F在线段BC中点时,求tanθ.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)取DS中点为G,连接GE,GF,则GE∥BD,取AS的中点H,连接BH,取GM=BF,利用勾股定理BF的长度;
(Ⅱ)求出S△AFB=
•4•2=4,S△EAF=
•2
•2
=2
,可得cosθ=
,即可求出tanθ.
(Ⅱ)求出S△AFB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
| 4 | ||
2
|
解答:
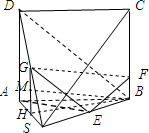 解:(Ⅰ)取DS中点为G,连接GE,GF,则GE∥BD,
解:(Ⅰ)取DS中点为G,连接GE,GF,则GE∥BD,
∵EF⊥BD,∴GE⊥FE,
取AS的中点H,连接BH,取GM=BF,则设BF=x,
∵△SAB是正三角形,四边形ABCD为正方形,AB=BC=4,
∴GF2=(2-x)2+(2
)2=(2
)2+22+x2,
∴x=1;
(Ⅱ)当点F在线段BC中点时,S△AFB=
•4•2=4,
△EAF中,AE=2
,EF=2
,AE⊥EF,S△EAF=
•2
•2
=2
,
∴cosθ=
,
∴sinθ=
,
∴tanθ=
.
 解:(Ⅰ)取DS中点为G,连接GE,GF,则GE∥BD,
解:(Ⅰ)取DS中点为G,连接GE,GF,则GE∥BD,∵EF⊥BD,∴GE⊥FE,
取AS的中点H,连接BH,取GM=BF,则设BF=x,
∵△SAB是正三角形,四边形ABCD为正方形,AB=BC=4,
∴GF2=(2-x)2+(2
| 3 |
| 2 |
∴x=1;
(Ⅱ)当点F在线段BC中点时,S△AFB=
| 1 |
| 2 |
△EAF中,AE=2
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
∴cosθ=
| 4 | ||
2
|
∴sinθ=
2
| ||
2
|
∴tanθ=
| ||
| 2 |
点评:本题考查面面垂直,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
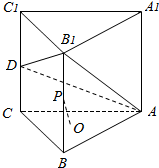 三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D.
三棱柱ABC-A1B1C1中,点D、P为棱CC1、BB1的中点,O为△ABC重心,求证:OP∥平面AB1D. 在正方体ABCD-A1B1C1D1中.
在正方体ABCD-A1B1C1D1中.