题目内容
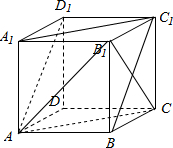
 在正方体ABCD-A1B1C1D1中.
在正方体ABCD-A1B1C1D1中.(1)证明:AC∥平面A1BC1;
(2)在正方体中,求DC1与B1C直线所组成的角的大小;
(3)在正方体ABCD-A1B1C1D1中,求证BC1∥平面AD1C.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:综合题,空间位置关系与距离
分析:(1)连接AC,A1C1,则A1C1∥AC,利用线面平行的判定定理即可证明;
(2)连接AB1,则AB1∥DC1,∠AB1C为DC1与B1C直线所组成的角;
(3)连接AD1,则AD1∥BC1,利用线面平行的判定定理即可证明.
(2)连接AB1,则AB1∥DC1,∠AB1C为DC1与B1C直线所组成的角;
(3)连接AD1,则AD1∥BC1,利用线面平行的判定定理即可证明.
解答:
 (1)证明:连接AC,A1C1,则A1C1∥AC,
(1)证明:连接AC,A1C1,则A1C1∥AC,
∵AC?平面A1BC1,A1C1?平面A1BC1,
∴AC∥平面A1BC1;
(2)解:连接AB1,则AB1∥DC1,
∴∠AB1C为DC1与B1C直线所组成的角,
∵△AB1C是等边三角形,
∴∠AB1C=60°,
∴DC1与B1C直线所组成的角的大小为60°;
(3)证明:连接AD1,
∵AD1∥BC1,BC1?平面AD1C,AD1?平面AD1C,
∴BC1∥平面AD1C.
 (1)证明:连接AC,A1C1,则A1C1∥AC,
(1)证明:连接AC,A1C1,则A1C1∥AC,∵AC?平面A1BC1,A1C1?平面A1BC1,
∴AC∥平面A1BC1;
(2)解:连接AB1,则AB1∥DC1,
∴∠AB1C为DC1与B1C直线所组成的角,
∵△AB1C是等边三角形,
∴∠AB1C=60°,
∴DC1与B1C直线所组成的角的大小为60°;
(3)证明:连接AD1,
∵AD1∥BC1,BC1?平面AD1C,AD1?平面AD1C,
∴BC1∥平面AD1C.
点评:本题考查线面平行,考查线线角,考查学生分析解决问题的能力,比较综合.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2. 如图,四棱锥S-ABCD中,△SAB是正三角形,四边形ABCD为正方形,平面SAB⊥平面ABCD,AB=BC=4,E为SB中点,点F在线段BC上.
如图,四棱锥S-ABCD中,△SAB是正三角形,四边形ABCD为正方形,平面SAB⊥平面ABCD,AB=BC=4,E为SB中点,点F在线段BC上.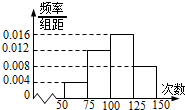 为了了解初中生的身体素质,某地区随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是10,则n的值为
为了了解初中生的身体素质,某地区随机抽取了n名学生进行跳绳测试,根据所得数据画样本的频率分布直方图如图所示,且从左到右第一小组的频数是10,则n的值为