题目内容
设方程x2+y2-2mx-2m2y+m4+2m2-m=0表示一个圆.
(1)求m的取值范围;
(2)m取何值时,圆的半径最大?并求出最大半径.
(1)求m的取值范围;
(2)m取何值时,圆的半径最大?并求出最大半径.
考点:二元二次方程表示圆的条件
专题:直线与圆
分析:(1)将圆的方程化为标准方程,利用方程为圆,可得半径大于0,即可得到m的范围‘
(2)设r2=-m2+m,在(1)求出的m的范围中,利用二次函数求最值的方法求出半径的最大值即可.
(2)设r2=-m2+m,在(1)求出的m的范围中,利用二次函数求最值的方法求出半径的最大值即可.
解答:
解:(1)由方程x2+y2-2mx-2m2y+m4+2m2-m=0,
变形得:(x-m)2+(y-m2)2=-m2+m,
要使方程表示圆,则需要-m2+m>0,∴m2-m<0,∴0<m<1;
(2)设r2=-m2+m=-(m-
)2+
∵0<m<1,
∴当m=
时,r2最大为
,圆的半径最大为
.
变形得:(x-m)2+(y-m2)2=-m2+m,
要使方程表示圆,则需要-m2+m>0,∴m2-m<0,∴0<m<1;
(2)设r2=-m2+m=-(m-
| 1 |
| 2 |
| 1 |
| 4 |
∵0<m<1,
∴当m=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查方程表示圆时的条件,考查二次函数的最大值,将圆的一般方程化为标准方程是关键.

练习册系列答案
相关题目
已知函数f(x)=ax4+bx3+cx2+dx+e,(a,b,c,d,e∈R,且a≠0)的四个零点构成公差为2的等差数列,则f′(x)的所有零点中最大值与最小值之差是( )
| A、4 | ||
B、
| ||
| C、2 | ||
D、2
|
若函数f(x)=2x-mx在区间(-1,0)内有一个零点,则实数m的取值可以是( )
| A、-1 | ||
| B、1 | ||
C、.-
| ||
D、
|
函数y=cos2x+2asinx在区间[-
,π]上的最大值为2,则实数a的值为( )
| π |
| 6 |
A、1或 -
| ||
B、-
| ||
C、
| ||
D、1或
|
一个几何体的三视图如右图所示,则该几何体的体积是( )


A、
| ||
B、
| ||
| C、1 | ||
D、
|
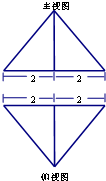 三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形,其中底边长为4,腰长为3,则该三棱锥左视图的面积为( )
三棱锥P-ABC的主视图和俯视图为如图所示的两个全等的等腰三角形,其中底边长为4,腰长为3,则该三棱锥左视图的面积为( )