题目内容
4.S(A)表示集合A中所有元素的和,且A⊆{1,2,3,4,5},若S(A)能被3整除,则符合条件的非空集合A的个数是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
分析 利用列举法能求出符合条件的非空集合A的个数.
解答 解:由题意得符合条件的非空集合A有:
{3},{1,2},{1,5},{2,4},{4,5},{1,2,3},{1,3,5},{2,3,4},
{3,4,5},{1,2,4,5},{1,2,3,4,5},共有11个.
故选:B.
点评 本题考查符合条件的非空集合A的个数的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
15.i为虚数单位,则i+i2+i3+i4=( )
| A. | 0 | B. | i | C. | 2i | D. | -i |
16.已知集合A={-1,0,1,2,3},B={x|x<2},则A∩B=( )
| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1,2,3} | D. | {-1,0,1,2,3} |
13.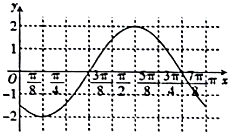 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{7π}{12}$ |
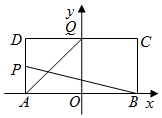 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.