题目内容
18.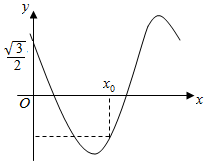 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )| A. | φ=$\frac{π}{6}$,x0=1 | B. | φ=$\frac{π}{6}$,x0=$\frac{4}{3}$ | C. | φ=$\frac{π}{3}$,x0=1 | D. | φ=$\frac{π}{3}$,x0=$\frac{2}{3}$ |
分析 根据f(0)=$\frac{\sqrt{3}}{2}$解出φ,利用f(x0)=-f(0)=-$\frac{\sqrt{3}}{2}$解出x0.
解答 解:由函数图象可知f(0)=$\frac{\sqrt{3}}{2}$,即cosφ=$\frac{\sqrt{3}}{2}$,
∵0<φ<$\frac{π}{2}$,∴φ=$\frac{π}{6}$.
∵f(x0)=-f(0)=-$\frac{\sqrt{3}}{2}$,
∴cos($π{x}_{0}+\frac{π}{6}$)=-$\frac{\sqrt{3}}{2}$.
∴$π{x}_{0}+\frac{π}{6}$=$\frac{7π}{6}$,解得x0=1.
故选:A.
点评 本题考查了余弦函数的图象与性质,属于基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
8.设平面向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=2、|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点P满足$\overrightarrow{OP}=\frac{m}{{\sqrt{2{m^2}+2{n^2}}}}\overrightarrow{OA}+\frac{{\sqrt{2}n}}{{\sqrt{{m^2}+{n^2}}}}\overrightarrow{OB}$,其中m≥0,n≥0,则点P所表示的轨迹长度为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{{\sqrt{2}π}}{2}$ |
9.某城区按以下规定收取水费:若每月用水不超过20m3,则每立方米水费按2元收取;若超过20m3,则超过的部分按每立方米3元收取,如果某户居民在某月所交水费的平均价为每立方米2.20元,则这户居民这月共用水( )
| A. | 46m3 | B. | 44m3 | C. | 26m3 | D. | 25m3 |
13.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的左、右焦点分别为F1、F2,过F2的直线与该双曲线的右支交于A、B两点,若△ABF1的周长为30,则点F1与以AB为直径的圆的位置关系为( )
| A. | 在圆外 | B. | 在圆上 | C. | 在圆内 | D. | 无法确定 |
8.若函数f(x)=cos(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<0)的最小正周期为π,且其图象过点($\frac{5π}{12}$,0),则f(x)的图象的一条对称轴方程为( )
| A. | x=$\frac{π}{3}$ | B. | x=$\frac{2π}{3}$ | C. | x=$\frac{π}{6}$ | D. | x=-$\frac{2π}{3}$ |