题目内容
13.已知双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的左、右焦点分别为F1、F2,过F2的直线与该双曲线的右支交于A、B两点,若△ABF1的周长为30,则点F1与以AB为直径的圆的位置关系为( )| A. | 在圆外 | B. | 在圆上 | C. | 在圆内 | D. | 无法确定 |
分析 求得双曲线的a,b,c,设|AF2|=m,|BF2|=n,运用双曲线的定义求得|AF1|,|BF1|,由题意可得|AB|=11,考虑双曲线的垂直于x轴的弦的长度,比较AB的中点与点F1的距离与AB的一半的大小关系,即可得到结论.
解答 解:双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1的a=2,b=3,c=$\sqrt{13}$,
设|AF2|=m,|BF2|=n,
由双曲线的定义可得|AF1|=2a+m=4+m,|BF1|=2a+n=4+n,
由题意可得△ABF1的周长为|AF1|+|AF2|+|BF1|+|BF2|=30,
即有8+2(m+n)=30,即为m+n=11,即|AB|=11,
又x=c=$\sqrt{13}$,解得y=±3$\sqrt{\frac{13}{4}-1}$=±$\frac{9}{2}$,
即有过F2垂直于x轴的弦长为9,
则F1到AB的中点的距离d>2c=2$\sqrt{13}$>$\frac{11}{2}$,
可得点F1与以AB为直径的圆的位置关系为在圆外.
故选:A.
点评 本题考查双曲线的定义、方程和性质,主要考查定义法的运用和点与圆的位置关系的判断,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
4.实数x,y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤1}\end{array}\right.$,则z=$\frac{y}{x-2}$的最小值为( )
| A. | -$\frac{1}{4}$ | B. | 1 | C. | -1 | D. | 0 |
1.已知命题p1:函数y=($\frac{1}{2}$)x-($\frac{1}{2}$)-x在R上为减函数,p2:函数y=($\frac{1}{2}$)x+($\frac{1}{2}$)-x在R上为增函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是( )
| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
8.设数列{an}的前n项和为Sn,若$\frac{{S}_{n}}{{S}_{2n}}$为常数,则称数列{an}为“吉祥数列“,己知等差数列{bn}的首项为1,公差不为0,若数列{bn}为“吉祥数列“,则数列{bn}的通项公式为( )
| A. | bn=n-1 | B. | bn=2n-1 | C. | bn=n+1 | D. | bn=2n+1 |
18.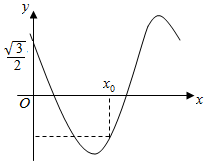 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )| A. | φ=$\frac{π}{6}$,x0=1 | B. | φ=$\frac{π}{6}$,x0=$\frac{4}{3}$ | C. | φ=$\frac{π}{3}$,x0=1 | D. | φ=$\frac{π}{3}$,x0=$\frac{2}{3}$ |
2.在下列选项中,解集为{x|x<-1或x>5}的不等式是( )
| A. | (x+1)(x-5)<0 | B. | (x-1)(x+5)<0 | C. | (x-1)(x+5)>0 | D. | (x+1)(x-5)>0 |