题目内容
9．某城区按以下规定收取水费：若每月用水不超过20m3，则每立方米水费按2元收取；若超过20m3，则超过的部分按每立方米3元收取，如果某户居民在某月所交水费的平均价为每立方米2.20元，则这户居民这月共用水（ ）| A． | 46m3 | B． | 44m3 | C． | 26m3 | D． | 25m3 |
分析 设他这个月共用了x立方米的水，依据钱数不变可列方程，依据等式的性质即可求解．
解答 解：设他这个月共用了x立方米的水
20×2+（x-20）×3=2.2x
40+3x-60=2.2x
0.8x=20
x=25．
他这个月共用了25立方米的水．
故选：D．
点评 解答本题用方程比较容易理解，只要依据数量间的等量关系，列出方程，再根据等式的性质即可求解．
练习册系列答案
相关题目
4．实数x，y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤1}\end{array}\right.$，则z=$\frac{y}{x-2}$的最小值为（ ）
| A． | -$\frac{1}{4}$ | B． | 1 | C． | -1 | D． | 0 |
1．已知命题p1：函数y=（$\frac{1}{2}$）x-（$\frac{1}{2}$）-x在R上为减函数，p2：函数y=（$\frac{1}{2}$）x+（$\frac{1}{2}$）-x在R上为增函数，则在命题q1：p1∨p2，q2：p1∧p2，q3：（￢p1）∨p2和q4：p1∧（￢p2）中，真命题是（ ）
| A． | q1，q3 | B． | q2，q3 | C． | q1，q4 | D． | q2，q4 |
18．
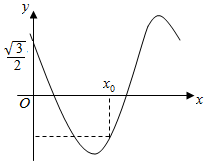已知函数f（x）=cos（πx+φ）（0＜φ＜$\frac{π}{2}$）的部分图象如图所示，f（x0）=-f（0），则正确的选项是（ ）
已知函数f（x）=cos（πx+φ）（0＜φ＜$\frac{π}{2}$）的部分图象如图所示，f（x0）=-f（0），则正确的选项是（ ）| A． | φ=$\frac{π}{6}$，x0=1 | B． | φ=$\frac{π}{6}$，x0=$\frac{4}{3}$ | C． | φ=$\frac{π}{3}$，x0=1 | D． | φ=$\frac{π}{3}$，x0=$\frac{2}{3}$ |