题目内容
10.实数x,y满足$\left\{\begin{array}{l}{y-2x≤-2}\\{y≥1}\\{x+y≤4}\end{array}\right.$,则$\frac{{x}^{2}+{y}^{2}}{xy}$的取值范围是[2,$\frac{10}{3}$].分析 作出不等式组对应的平面区域,利用换元法结合分式的性质,利用数形结合是解决本题的关键.
解答  解:作出不等式组对应的平面区域如图
解:作出不等式组对应的平面区域如图
则x>0,y>0,
则$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{1+(\frac{y}{x})^{2}}{\frac{y}{x}}$,
设k=$\frac{y}{x}$,
则$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{1+(\frac{y}{x})^{2}}{\frac{y}{x}}$=$\frac{1+{k}^{2}}{k}$=k+$\frac{1}{k}$.
k的几何意义为区域内的点到原点的斜率,
由图象知OA的斜率最大,OB的斜率最小,
由$\left\{\begin{array}{l}{y-2x=-2}\\{x+y=4}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即A(2,2),
由$\left\{\begin{array}{l}{y=1}\\{x+y=4}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,即B(3,1),
则OA的斜率k=$\frac{2}{2}$=1,OB的斜率k=$\frac{1}{3}$,
则$\frac{1}{3}$≤k≤1,
∵z=k+$\frac{1}{k}$在$\frac{1}{3}$≤k≤1上是减函数,
∴z的最大值为$\frac{1}{3}+3$=$\frac{10}{3}$,z的最小值为1+1=2,
即2≤z≤$\frac{10}{3}$,
故答案为:[2,$\frac{10}{3}$]
点评 本题主要考查线性规划的应用,根据分式函数的性质,结合直线的斜率的几何意义是解决本题的关键.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
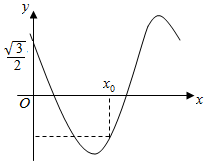 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )| A. | φ=$\frac{π}{6}$,x0=1 | B. | φ=$\frac{π}{6}$,x0=$\frac{4}{3}$ | C. | φ=$\frac{π}{3}$,x0=1 | D. | φ=$\frac{π}{3}$,x0=$\frac{2}{3}$ |
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
| A. | (x+1)(x-5)<0 | B. | (x-1)(x+5)<0 | C. | (x-1)(x+5)>0 | D. | (x+1)(x-5)>0 |