题目内容
6．已知数列{an}中a1+a2+a3+…+an=2n-1，求a12+a22+a32+…+an2的值．分析 由a1+a2+a3+…+an=2n-1，求出数列{an}是首项是1，公比是2的等比数列，进一步得到数列{an2}是等比数列，应用等比数列的前n项和公式得到结果．
解答 解：由a1+a2+a3+…+an=2n-1，得${S}_{n}={2}^{n}-1$，
当n=1时，a1=1，
当n≥2时，${a}_{n}={S}_{n}-{S}_{n-1}=（{2}^{n}-1）-（{2}^{n-1}-1）$=2n-1，
验证n=1时成立，
∴${a}_{n}={2}^{n-1}$，
则$\frac{{a}_{n+1}}{{a}_{n}}=\frac{{2}^{n}}{{2}^{n-1}}=2$，
∴数列{an}是首项是1，公比是2的等比数列，
则数列{an2}是首项是1，公比是4的等比数列，
∴a12+a22+a32+…+an2=$\frac{1×（1-{4}^{n}）}{1-4}=\frac{1}{3}（{4}^{n}-1）$．
点评 本题考查数列递推式，考查了等比关系的确定，训练了等比数列前n项和的求法，是中档题．
练习册系列答案
相关题目
1．已知命题p1：函数y=（$\frac{1}{2}$）x-（$\frac{1}{2}$）-x在R上为减函数，p2：函数y=（$\frac{1}{2}$）x+（$\frac{1}{2}$）-x在R上为增函数，则在命题q1：p1∨p2，q2：p1∧p2，q3：（￢p1）∨p2和q4：p1∧（￢p2）中，真命题是（ ）
| A． | q1，q3 | B． | q2，q3 | C． | q1，q4 | D． | q2，q4 |
11．设$\overrightarrow a$=（1，2），$\overrightarrow b$=（x，y），$\overrightarrow c$=$\overrightarrow a$+$\overrightarrow b$．若$\overrightarrow b$⊥$\overrightarrow c$，则点（x，y）的轨迹方程为（ ）
| A． | （x-$\frac{1}{2}$）2+（y-1）2=$\frac{5}{4}$ | B． | ${（x+\frac{1}{2}）^2}+{（y-1）^2}=\frac{5}{4}$ | C． | ${（x-\frac{1}{2}）^2}+{（y+1）^2}=\frac{5}{4}$ | D． | ${（x+\frac{1}{2}）^2}+{（y+1）^2}=\frac{5}{4}$ |
18．
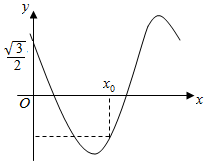已知函数f（x）=cos（πx+φ）（0＜φ＜$\frac{π}{2}$）的部分图象如图所示，f（x0）=-f（0），则正确的选项是（ ）
已知函数f（x）=cos（πx+φ）（0＜φ＜$\frac{π}{2}$）的部分图象如图所示，f（x0）=-f（0），则正确的选项是（ ）| A． | φ=$\frac{π}{6}$，x0=1 | B． | φ=$\frac{π}{6}$，x0=$\frac{4}{3}$ | C． | φ=$\frac{π}{3}$，x0=1 | D． | φ=$\frac{π}{3}$，x0=$\frac{2}{3}$ |
15．若α∈[-$\frac{π}{4}，\frac{π}{4}$]，β∈[-$\frac{π}{8}$，$\frac{π}{8}$]，且满足$\left\{\begin{array}{l}{{α}^{3}+sinα-2k=0}\\{4{β}^{3}+sinβcosβ+k=0}\end{array}\right.$，k∈R，则cos（α+2β）的值为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | 1 | D． | $\frac{1}{2}$ |