题目内容
8.若函数f(x)=cos(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<0)的最小正周期为π,且其图象过点($\frac{5π}{12}$,0),则f(x)的图象的一条对称轴方程为( )| A. | x=$\frac{π}{3}$ | B. | x=$\frac{2π}{3}$ | C. | x=$\frac{π}{6}$ | D. | x=-$\frac{2π}{3}$ |
分析 由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式,再利用余弦函数的图象的对称性,求得f(x)的图象的一条对称轴方程.
解答 解:若函数f(x)=cos(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<0)的最小正周期为π,
则$\frac{2π}{ω}$=π,求得ω=2,f(x)=cos(2x+φ).
根据它的图象过点($\frac{5π}{12}$,0),可得2•$\frac{5π}{12}$+φ=kπ+$\frac{π}{2}$,k∈Z,∴φ=kπ-$\frac{π}{3}$,∴φ=-$\frac{π}{3}$,
f(x)=cos(2x-$\frac{π}{3}$).
令2x-$\frac{π}{3}$=kπ,可得x=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
则f(x)的图象的一条对称轴方程为x=$\frac{π}{6}$,
故选:C.
点评 本题主要考查由函数y=Acos(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值;余弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
18.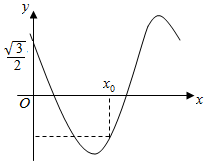 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )| A. | φ=$\frac{π}{6}$,x0=1 | B. | φ=$\frac{π}{6}$,x0=$\frac{4}{3}$ | C. | φ=$\frac{π}{3}$,x0=1 | D. | φ=$\frac{π}{3}$,x0=$\frac{2}{3}$ |
17.已知数列{an}为等比数列,a2,a4的等差中项为4,a5,a7的等差中项为8$\sqrt{2}$,则a1的值为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{4\sqrt{2}}{3}$ |
3.经过点M(2,1)作直线l交双曲线x2-$\frac{y^2}{2}$=1于A,B两点,且M为AB的中点,则直线l的方程为( )
| A. | 4x+y+7=0 | B. | 4x+y-7=0 | C. | 4x-y-7=0 | D. | 4x-y+7=0 |