题目内容
8.设平面向量$\overrightarrow{OA}$、$\overrightarrow{OB}$满足|$\overrightarrow{OA}$|=2、|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}•\overrightarrow{OB}$=0,点P满足$\overrightarrow{OP}=\frac{m}{{\sqrt{2{m^2}+2{n^2}}}}\overrightarrow{OA}+\frac{{\sqrt{2}n}}{{\sqrt{{m^2}+{n^2}}}}\overrightarrow{OB}$,其中m≥0,n≥0,则点P所表示的轨迹长度为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{{\sqrt{2}π}}{2}$ |
分析 根据条件可得到OA⊥OB,从而可分别以OA,OB为x轴,y轴,建立平面直角坐标系,从而可以得到$\overrightarrow{OA}=(2,0),\overrightarrow{OB}=(0,1)$,从而可得出向量$\overrightarrow{OP}$的坐标,可设P(x,y),从而可得到x2+y2=2(x≥0,y≥0),这样即可求出点P所表示的轨迹长度.
解答 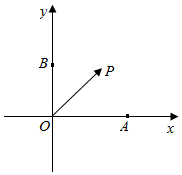 解:$\overrightarrow{OA}•\overrightarrow{OB}=0$;
解:$\overrightarrow{OA}•\overrightarrow{OB}=0$;
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$;
∴分别以OA,OB为x,y轴,建立如图所示平面直角坐标系,则:
A(2,0),B(0,1);
∴$\overrightarrow{OA}=(2,0),\overrightarrow{OB}=(0,1)$;
∴$\overrightarrow{OP}=(\frac{\sqrt{2}m}{\sqrt{{m}^{2}+{n}^{2}}},\frac{\sqrt{2}n}{\sqrt{{m}^{2}+{n}^{2}}})$,设P(x,y),$\overrightarrow{OP}=(x,y)$;
∴$\left\{\begin{array}{l}{x=\frac{\sqrt{2}m}{\sqrt{{m}^{2}+{n}^{2}}}}\\{y=\frac{\sqrt{2}n}{\sqrt{{m}^{2}+{n}^{2}}}}\end{array}\right.$;
∴x2+y2=2,(x≥0,y≥0);
∴P点的轨迹表示以原点为圆心,半径为$\sqrt{2}$的圆在第一象限的部分;
∴点P所表示的轨迹长度为$\frac{1}{4}•2π•\sqrt{2}=\frac{\sqrt{2}π}{2}$.
故选D.
点评 考查通过建立平面直角坐标系,利用向量坐标解决向量问题的方法,能求平面上点的坐标,根据点的坐标求向量的坐标,以及向量坐标的数乘运算,圆的标准方程,圆的周长公式.

| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
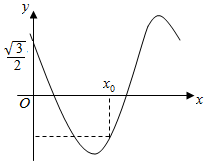 已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )
已知函数f(x)=cos(πx+φ)(0<φ<$\frac{π}{2}$)的部分图象如图所示,f(x0)=-f(0),则正确的选项是( )| A. | φ=$\frac{π}{6}$,x0=1 | B. | φ=$\frac{π}{6}$,x0=$\frac{4}{3}$ | C. | φ=$\frac{π}{3}$,x0=1 | D. | φ=$\frac{π}{3}$,x0=$\frac{2}{3}$ |