题目内容
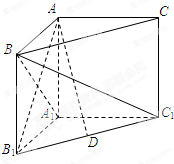 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.(Ⅰ)证明:AB1⊥平面A1BC1;
(Ⅱ)若点D为B1C1的中点,求AD与平面A1BC1所成角的大小.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)由题意所给的条件,结合线面垂直的判定定理可得结论;
(Ⅱ)确定AD,C1O的交点G为△AB1C1的重心,可得∠AGO是AD与平面A1BC1所成角,即可求出AD与平面A1BC1所成角的大小.
(Ⅱ)确定AD,C1O的交点G为△AB1C1的重心,可得∠AGO是AD与平面A1BC1所成角,即可求出AD与平面A1BC1所成角的大小.
解答:
(Ⅰ)证明:∵AA1⊥平面A1B1C1,∴AA1⊥A1C1.
又 A1C1⊥A1B1,AA1∩A1B1=A1
∴A1C1⊥平面AA1B1B.
∴A1C1⊥AB1
又四边形AA1B1B是正方形,AB1⊥A1B,A1B∩A1C1=A1
∴AB1⊥平面A1BC1.
(Ⅱ)设AB1∩BA1=O,连结AC1,
∵AB=AC=AA1=a,A1C1⊥A1B1,AA1⊥平面A1B1C1,
∴△AB1C1是正三角形,
∵AD,C1O是△AB1C1的中线,
∴AD,C1O的交点G为△AB1C1的重心,
∴∠AGO是AD与平面A1BC1所成角,
在Rt△AOG中,AG=
AD=
AB,AO=
AB,
∴sin∠AGO=
,∴∠AGO=60°,即AD与平面A1BC1所成角为60°.
又 A1C1⊥A1B1,AA1∩A1B1=A1
∴A1C1⊥平面AA1B1B.
∴A1C1⊥AB1
又四边形AA1B1B是正方形,AB1⊥A1B,A1B∩A1C1=A1
∴AB1⊥平面A1BC1.
(Ⅱ)设AB1∩BA1=O,连结AC1,
∵AB=AC=AA1=a,A1C1⊥A1B1,AA1⊥平面A1B1C1,
∴△AB1C1是正三角形,
∵AD,C1O是△AB1C1的中线,
∴AD,C1O的交点G为△AB1C1的重心,
∴∠AGO是AD与平面A1BC1所成角,
在Rt△AOG中,AG=
| 2 |
| 3 |
| ||
| 3 |
| ||
| 2 |
∴sin∠AGO=
| ||
| 2 |
点评:本题考查直线与平面所成的角,考查线面垂直的判定,属中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若a=0是a(a-1)=0的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
 如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )
如图,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图的周长是( )| A、8 cm | ||
| B、6 cm | ||
C、2(1+
| ||
D、2(1+2
|
若向量
=(1,λ,1),
=(2,-1,1)且
与
的夹角的余弦值为
,则λ等于( )
| a |
| b |
| a |
| b |
| 1 |
| 6 |
| A、2 | ||
| B、-2 | ||
C、-2或
| ||
D、2或
|
方程x2+(m-3)x+m=0有两个正实数根,则m的取值范围是( )
| A、0≤m<1 |
| B、0<m<1 |
| C、0<m≤1 |
| D、0≤m≤1 |
 三棱锥P-ABC中,已知PC=10,AB=8,E、F分别为PA、BC的中点,EF=
三棱锥P-ABC中,已知PC=10,AB=8,E、F分别为PA、BC的中点,EF=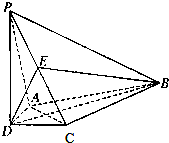 如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.
如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.