题目内容
方程x2+(m-3)x+m=0有两个正实数根,则m的取值范围是( )
| A、0≤m<1 |
| B、0<m<1 |
| C、0<m≤1 |
| D、0≤m≤1 |
考点:一元二次方程的根的分布与系数的关系
专题:计算题,不等式的解法及应用
分析:由已知中关于x的方程x2+(m-3)x+m=0的两个实数根是正数,则方程的△≥0,且方程的两根x1,x2满足x1+x2>0,x1•x2>0,由此构造一个关于m的不等式组,解不等式组即可得到实数m的取值范围.
解答:
解:若关于x的方程x2+(m-3)x+m=0的两个实数根是正数,
即x1>0,x2>0,
则
,即有
,
解得0<m≤1.
故实数m的取值范围是(0,1]
故选C.
即x1>0,x2>0,
则
|
|
解得0<m≤1.
故实数m的取值范围是(0,1]
故选C.
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,韦达定理,其中根据已知条件,结合一元二次方程的根的个数与△的关系及韦达定理,构造一个关于m的不等式组,是解答本题的关键.

练习册系列答案
相关题目
| A | 2 8 |
| A、10 | B、30 | C、56 | D、120 |
圆x2+y2-2x-2y+1=0和圆x2+y2-8x-10y+25=0的位置关系是( )
| A、相交 | B、外切 | C、内切 | D、相离 |
下列各式中错误的是( )
| A、30.9>30.8 | ||||
| B、log0.50.4>log0.50.5 | ||||
| C、0.65-0.1<0.650.1 | ||||
D、3 -
|
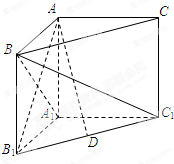 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.