题目内容
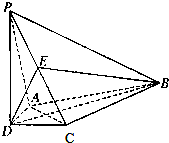 如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.
如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.(1)证明:PA∥平面BDE;
(2)证明:AC⊥平面PBD.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)证明:设AC∩BD=H,连结EH.证明EH∥PA.利用直线与平面平行的判定定理证明PA∥平面BDE.
(2)证明PD⊥AC.DB⊥AC.通过直线与平面垂直的判定定理证明AC⊥平面PBD.
(2)证明PD⊥AC.DB⊥AC.通过直线与平面垂直的判定定理证明AC⊥平面PBD.
解答:
(1)证明:设AC∩BD=H,连结EH.
在△ADC中,∵AD=CD,且DB平分∠ADC,
∴H为AC的中点.
又由题设,E为PC的中点,故EH∥PA.
又EH⊆平面BDE,且PA?平面BDE,
∴PA∥平面BDE.…(6分)
(2)证明:∵PD⊥平面ABCD,AC⊆平面ABCD,∴PD⊥AC.
由(1)可得,DB⊥AC.
又PD∩DB=D,故AC⊥平面PBD.…(12分)
在△ADC中,∵AD=CD,且DB平分∠ADC,
∴H为AC的中点.
又由题设,E为PC的中点,故EH∥PA.
又EH⊆平面BDE,且PA?平面BDE,
∴PA∥平面BDE.…(6分)
(2)证明:∵PD⊥平面ABCD,AC⊆平面ABCD,∴PD⊥AC.
由(1)可得,DB⊥AC.
又PD∩DB=D,故AC⊥平面PBD.…(12分)
点评:本题考查直线与平面平行与垂直的判定定理的应用,考查逻辑推理能力.

练习册系列答案
相关题目
若直线a与平面α垂直,那么平面α与直线a平行的直线有( )
| A、0条 | B、0条或无数条 |
| C、无数条 | D、不确定 |
 据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )
据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20-80mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.据《法制晚报》报道,2012年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为( )| A、4320 | B、2880 |
| C、8640 | D、2160 |
一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是(1,0,0),(0,0,1),(0,1,0),(1,1,1),画该四面体三视图中的正视图时,以zOy平面为投影面,则得到的正视图可为( )
A、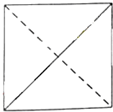 |
B、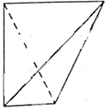 |
C、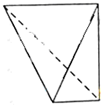 |
D、 |
| A | 2 8 |
| A、10 | B、30 | C、56 | D、120 |
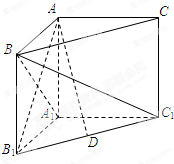 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面A1B1C1,AB=AC=AA1.