题目内容
已知角α的终边经过点P(-5,12),则sin(-π-α)-2cos(π-α)的值为 .
考点:运用诱导公式化简求值,任意角的三角函数的定义
专题:三角函数的求值
分析:利用三角函数的定义,求出sinα,cosα的值,即可求解结果.
解答:
解:角α的终边经过点P(-5,12),
由三角函数的定义可知:sinα=
,cosα=-
∴sin(-π-α)-2cos(π-α)=sinα+2cosα=
;
故答案为:
.
由三角函数的定义可知:sinα=
| 12 |
| 13 |
| 5 |
| 13 |
∴sin(-π-α)-2cos(π-α)=sinα+2cosα=
| 2 |
| 13 |
故答案为:
| 2 |
| 13 |
点评:本题考查任意角的三角函数的定义,基本知识的考查.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
cos(-2040°)的值为( )
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|
已知实数x,y满足:
,则z=2|x|+y的取值范围是( )
|
| A、[0,11] |
| B、[-5,11] |
| C、[-1,11] |
| D、[1,11] |
设a,b是两条不同直线,α,β是两个不同平面,下列四个命题中正确的是( )
| A、若a,b与α所成的角相等,则a∥b |
| B、若a∥α,b∥β,α∥β,则a∥b |
| C、若a⊥α,b⊥β,α⊥β,则a⊥b |
| D、若a?α,b?β,a∥b,则α∥β |
 如图,D为△ABC的边BC中点,E在AC上且AE=3,EC=2,AD交BE于F,那么
如图,D为△ABC的边BC中点,E在AC上且AE=3,EC=2,AD交BE于F,那么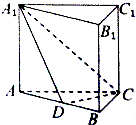 如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为
如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为