题目内容
函数y=f(x)的图象平移向量
=(a1,a2)得到函数的图象解析式是 .
| a |
考点:函数解析式的求解及常用方法
专题:作图题
分析:根据向量
=(a1,a2)的方向,利用函数图象变换的理论,得变换后函数解析式即可.
| a |
解答:
解:设(x1,y1)是f(x)上的一点,平移后是(x,y),
∴x-x1=a1,x1=x-a1,
y-y1=a2,y1=y-a2;
又∵y1=f(x1),
∴y-a2=f(x-a1),即y=f(x-a1)+a2;
∴平移后的解析式为:y=f(x-a1)+a2;
故答案为:y=f(x-a1)+a2.
∴x-x1=a1,x1=x-a1,
y-y1=a2,y1=y-a2;
又∵y1=f(x1),
∴y-a2=f(x-a1),即y=f(x-a1)+a2;
∴平移后的解析式为:y=f(x-a1)+a2;
故答案为:y=f(x-a1)+a2.
点评:本题考察了函数图象的平移变换,向量平移与图象平移变换的关系,掌握平移方向和平移量是解决本题的关键

练习册系列答案
相关题目
已知函数f(x)=xsinx,记m=f(-
),n=f(
),则下列关系正确的是( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、m<0<n |
| B、0<n<m |
| C、0<m<n |
| D、n<m<0 |
曲线y=2x4上的点到直线y=-x-1的距离的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若x,y均为区间(0,1)的随机数,则2x-y>0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
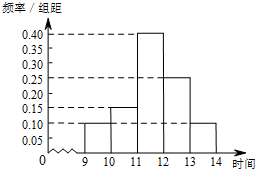 某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )| A、8万元 | B、10万元 |
| C、12万元 | D、15万 |