题目内容
11.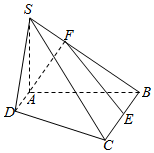 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且AB=4,SA=3.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且AB=4,SA=3.(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),当∠AFE=90°时,求$\frac{SF}{FB}$的值.
分析 (1)通过平面SAB内的直线BC垂直平面SAB,利用平面与平面垂直的判定定理证明:平面SBC⊥平面SAB.
(2)推导出AF⊥EF,BC⊥AF,AF⊥BS,分别求出SF,FB,由此能求出$\frac{SF}{FB}$.
解答 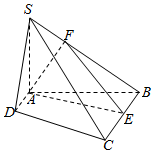 证明:(1)∵SA⊥平面ABCD,∴SA⊥BC,
证明:(1)∵SA⊥平面ABCD,∴SA⊥BC,
∵底面ABCD为直角梯形,AD∥BC,∠BAD=90°,∴BC⊥AB,
∵SA∩AB=A,∴BC⊥平面SAB,
∵BC?平面SAB,∴平面SBC⊥平面SAB.
解:(2)∵∠AFE=90°,∴AF⊥EF,
由(1)可知,BC⊥平面SAB,
∵AF?平面SAB,∴BC⊥AF,
∵EF∩BC=E,EF?平面SBC,∴AF⊥平面SBC,∴AF⊥BS,
在Rt△SAB中,AB=4,SA=3,∴BS=5,∴SF=$\frac{S{A}^{2}}{BS}$=$\frac{9}{5}$,
∴FB=5-$\frac{9}{5}$=$\frac{16}{5}$,
∴$\frac{SF}{FB}$=$\frac{9}{16}$.
点评 本题考查平面与平面垂直的判定定理的应用,直线与平面平行与垂直的判定定理的应用,考查空间想象能力,逻辑推理能力,分析问题解决问题的能力.

练习册系列答案
相关题目
19.已知tanα=-2,cosα>0,则sin(π-α)等于( )
| A. | -$\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{2\sqrt{5}}{5}$ | D. | ±$\frac{2\sqrt{5}}{5}$ |