题目内容
20.sin$\frac{π}{18}$•cos$\frac{2π}{9}$•sin(-$\frac{11π}{18}$)=-$\frac{1}{8}$.分析 把把原式都换成余弦函数,得到原式=-$cos\frac{4π}{9}cos\frac{2π}{9}cos\frac{π}{9}$,再由$cosα=\frac{sin2α}{2sinα}$,能求出结果.
解答 解:sin$\frac{π}{18}$•cos$\frac{2π}{9}$•sin(-$\frac{11π}{18}$)
=-$cos\frac{4π}{9}cos\frac{2π}{9}cos\frac{π}{9}$
=-$\frac{sin\frac{8π}{9}}{2sin\frac{4π}{9}}$×$\frac{sin\frac{4π}{9}}{2sin\frac{2π}{9}}$×$\frac{sin\frac{2π}{9}}{2sin\frac{π}{9}}$
=-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$
=-$\frac{1}{8}$.
故答案为:-$\frac{1}{8}$.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意诱导公式和二倍角公式的合理运用.

练习册系列答案
相关题目
3.已知i是虚数单位,若复数(a+i)(2-i)是纯虚数,则实数a等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
10.若命题“?x∈R,使得sinxcosx>m”是真命题,则m的值可以是( )
| A. | -$\frac{1}{3}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2}{3}$ |
7.不等式x2+2x-3≤0的解集为( )
| A. | [-1,3] | B. | [-3,-1] | C. | [-3,1] | D. | [1,3] |
8.设函数f(x)=sin2x+$\sqrt{3}cos2x$+$\frac{π}{6}$的图象关于点(x0,y0)成中心对称,且x0$∈(\frac{π}{2},π)$,则x0+y0=( )
| A. | π | B. | $\frac{π}{2}$ | C. | $π或\frac{π}{2}$ | D. | 0或$\frac{π}{2}$ |
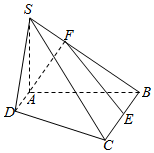 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且AB=4,SA=3.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,且AB=4,SA=3.