已知tanα=-2.cosα＞0.则sinA．-$\frac{\sqrt{5}}{5}$B．$\frac{2\sqrt{5}}{5}$C．-$\frac{2\sqrt{5}}{5}$D．±$\frac{2\sqrt{5}}{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

19．已知tanα=-2，cosα＞0，则sin（π-α）等于（　　）

A．

-$\frac{\sqrt{5}}{5}$

B．

$\frac{2\sqrt{5}}{5}$

C．

-$\frac{2\sqrt{5}}{5}$

D．

±$\frac{2\sqrt{5}}{5}$

分析由已知及同角三角函数基本关系可知sinα，利用诱导公式即可求值．

解答解：∵tanα=-2，cosα＞0，
∴sinα=-$\frac{2}{\sqrt{5}}$=-$\frac{2\sqrt{5}}{5}$，
∴sin（π-α）=sinα=-$\frac{2\sqrt{5}}{5}$．
故选：C．

点评本题主要考查同角三角函数基本关系的运用，属于基本知识的考查．

练习册系列答案

10．正数数列{a_n}中，a₁=3，a_n+1=ba_n+1（b是常数，n=1，2，3，…），且a₁-1，a₂+1，a₃-1成等差数列．
（1）求b的值；
（2）求数列{a_n}的前n项和S_n．

7．函数y=$\frac{sinx+1}{cosx+3}$的值域为[0，$\frac{3}{4}$]．

14．某物体的运动方程是S=3t²-5t+1（s表示位移，t表示时刻），那么下列说法中正确的序号是：②③④．
①此物体按匀速直线运动；②此物体在t=2时的位移为3；③此物体在t=3时的速度为13；④此物体在任何时刻的加速度都是6；⑤位移在不同时刻的瞬时变化率各不相同．

4．已知sin（$\frac{π}{3}$+a）=$\frac{12}{13}$，a∈（$\frac{π}{6}$，$\frac{2π}{3}$），则cosα的值为（　　）

A．

$\frac{12\sqrt{3}-5}{13}$

B．

$\frac{12\sqrt{3}-5}{26}$

C．

$\frac{12\sqrt{3}+5}{13}$

D．

$\frac{12\sqrt{3}+5}{26}$

11．

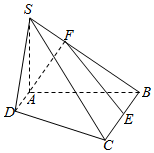如图，在四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，且AB=4，SA=3．
（1）求证：平面SBC⊥平面SAB；
（2）若E、F分别为线段BC、SB上的一点（端点除外），当∠AFE=90°时，求$\frac{SF}{FB}$的值．

8．已知函数f（x）=sin$\frac{πx}{2}$（x∈R），任取t∈R，若函数f（x）在区间[t，t+1]上的最大值为M（t），最小值为m（t），记g（t）=M（t）-m（t）．
（1）求函数f（x）的最小正周期及对称轴方程；
（2）当t∈[-2，0]时，求函数g（t）的解析式．

7．不等式x²+2x-3≤0的解集为（　　）

试题分类