题目内容
计算求值：
（1）计算
（sin
+cos
）2dx；
（2）已知复数z满足z•
-i（
）=1-（
），求z．
（1）计算
| ∫ |
0 |
| x |
| 2 |
| x |
| 2 |
（2）已知复数z满足z•
. |
| z |
. |
| 3z |
. |
| 3i |
考点：复数代数形式的混合运算,微积分基本定理
专题：数系的扩充和复数
分析：（1）把被积函数平方，然后展开，求出各被积函数的原函数，分别代入积分上限和下限后作差得答案；
（2）设出复数z，代入z•
-i（
）=1-（
），由复数相等的条件列式求解．
（2）设出复数z，代入z•
. |
| z |
. |
| 3z |
. |
| 3i |
解答：
解：（1）
(sin
+cos
)2dx
=
(1+sinx)dx
=
dx+
sinxdx
=
+[-cos
-(-cos0)]
=
+1；
（2）设z=a+bi（a，b∈R），
则由z•
-i（
）=1-（
），得
a2+b2-i[3（a-bi）]=1+3i．
∴a2+b2-3b-3ai=1+3i．
∴
．
解得：
或
．
∴z=-1或-1+3i．
| ∫ |
0 |
| x |
| 2 |
| x |
| 2 |
=
| ∫ |
0 |
=
| ∫ |
0 |
| ∫ |
0 |
=
| π |
| 2 |
| π |
| 2 |
=
| π |
| 2 |
（2）设z=a+bi（a，b∈R），
则由z•
. |
| z |
. |
| 3z |
. |
| 3i |
a2+b2-i[3（a-bi）]=1+3i．
∴a2+b2-3b-3ai=1+3i．
∴
|
解得：
|
|
∴z=-1或-1+3i．
点评：本题考查了微积分基本定理，考查了复数相等的条件，是基础的计算题．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
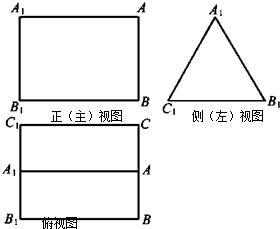如图是三棱柱ABC-A1B1C1的三视图，正（主）视图和俯视图都是矩形，侧（左）视图为等边三角形，D为AC的中点．
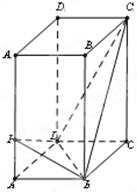如图，在正四棱柱ABCD-A1B1C1D1中，已知底面ABCD边长为2，侧棱AA1=6．