题目内容
设函数f(x)的定义域为D,若存在非零实数T使得对任意的x∈M(M⊆D),有x+T∈D,且f(x+T)≥f(x),则称函数f(x)为M上的T高调函数.
(1)现给出下列命题:
①函数f(x)=log
x为(0,+∞)上的T高调函数;
②函数f(x)=sinx为R上的2π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).其中正确命题的序号是 ;
(2)如果定义域为R的函数f(x)是奇函数,当x≥0 时,f(x)=|x2-a2|-a2,且f(x)为R上的4高调函数,那么实数a的取值范围是 .
(1)现给出下列命题:
①函数f(x)=log
| 1 |
| 2 |
②函数f(x)=sinx为R上的2π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).其中正确命题的序号是
(2)如果定义域为R的函数f(x)是奇函数,当x≥0 时,f(x)=|x2-a2|-a2,且f(x)为R上的4高调函数,那么实数a的取值范围是
考点:命题的真假判断与应用,抽象函数及其应用
专题:函数的性质及应用,简易逻辑
分析:(1)①利用函数的单调性,直接判断正误即可.
②由正弦函数知函数f(x)=sin2x为R上的π高调函数;
③函数f(x)=x2为[-1,+∞)上m高调函数,只有[-1,1]上至少需要加2.
(2)定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,画出函数图象,可得4≥3a2-(-a2)⇒-1≤a≤1.
②由正弦函数知函数f(x)=sin2x为R上的π高调函数;
③函数f(x)=x2为[-1,+∞)上m高调函数,只有[-1,1]上至少需要加2.
(2)定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,画出函数图象,可得4≥3a2-(-a2)⇒-1≤a≤1.
解答:
(1)解:对于①,∵f(x)=log
x为减函数,函数f(x)=log
x不是(0,+∞)上的高调函数,∴①不正确;
对于②,∵sin(x+2π)≥sinx
∴函数f(x)=sinx为R上的2π高调函数,故②正确;
对于③,在[-1,+∞)上的任意x(设x=x+m)有y≥-1恒成立,则x+m≥-1恒成立,即m≥-1-x恒成立.
对于x∈[-1,+∞),当x=-1时-1-x最大为0,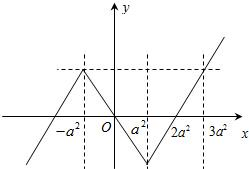
∴m≥0.
又∵f(x+m)≥f(x),即(x+m)2≥x2在x∈[-1,+∞)上恒成立,化简得m2+2mx≥0,
又∵m≥0,故m+2x≥0即m≥-2x恒成立,当x=-1时-2x最大为2,
∴m≥2,即实数m的取值范围是[2,+∞),故③正确;
(2)解:f(x)=|x-a2|-a2的图象如图,∴4≥3a2-(-a2)⇒-1≤a≤1.
实数a的取值范围是[-1,1].
故答案为:(1)②③;(2)[-1,1].
| 1 |
| 2 |
| 1 |
| 2 |
对于②,∵sin(x+2π)≥sinx
∴函数f(x)=sinx为R上的2π高调函数,故②正确;
对于③,在[-1,+∞)上的任意x(设x=x+m)有y≥-1恒成立,则x+m≥-1恒成立,即m≥-1-x恒成立.
对于x∈[-1,+∞),当x=-1时-1-x最大为0,

∴m≥0.
又∵f(x+m)≥f(x),即(x+m)2≥x2在x∈[-1,+∞)上恒成立,化简得m2+2mx≥0,
又∵m≥0,故m+2x≥0即m≥-2x恒成立,当x=-1时-2x最大为2,
∴m≥2,即实数m的取值范围是[2,+∞),故③正确;
(2)解:f(x)=|x-a2|-a2的图象如图,∴4≥3a2-(-a2)⇒-1≤a≤1.
实数a的取值范围是[-1,1].
故答案为:(1)②③;(2)[-1,1].
点评:考查学生的阅读能力,很应用知识分析解决问题的能力,考查数形结合的能力,用图解决问题的能力,属中档题.

练习册系列答案
相关题目
对于实数a和b,定义运算a*b,运算原理如图所示,则式子(
)-2*lne2的值为( )
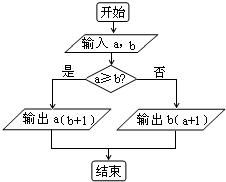
| 1 |
| 2 |

| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、y=2sin(
| ||||
B、y=2sin(2x-
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|