题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{5}(1-x)|,(x<1)}\\{-(x-2)^{2}+2,(x≥1)}\end{array}\right.$,则关于x的方程f(x+$\frac{1}{x}$-2)=a的实根个数构成的集合为{2,3,4,5,6,8}..分析 画出函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{5}(1-x)|,(x<1)}\\{-(x-2)^{2}+2,(x≥1)}\end{array}\right.$,的图象,判断x+$\frac{1}{x}$-2的范围,利用a的值,判断方程解的个数,即可得到方程f(x+$\frac{1}{x}$-2)=a的实根个数构成的集合.
解答 解:函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{5}(1-x)|,(x<1)}\\{-(x-2)^{2}+2,(x≥1)}\end{array}\right.$的图象,如图:当x>1时,x+$\frac{1}{x}$-2>0,当x=1时,x$+\frac{1}{x}$-2=0,
当x∈(0,1)时,x+$\frac{1}{x}$-2>0,
当x<0时,x+$\frac{1}{x}$-2<0,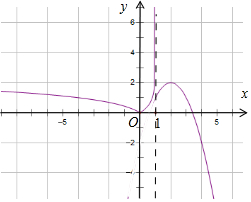
当a<0或a>2时,函数y=f(x+$\frac{1}{x}$-2)与y=a,由一个交点,此时方程有两个x值,满足题意.
当a=0时,函数有两个交点,满足方程的解由x=0,与x>0的两个解,此时解的集合为:3个;
a=2时,方程有4个解.
a∈(1,2)时,方程有8个解.
a=1时,方程有6个解.
a∈(0,1),方程有5个解.
关于x的方程f(x+$\frac{1}{x}$-2)=a的实根个数构成的集合为:{2,3,4,5,6,8}.
故答案为:{2,3,4,5,6,8}.
点评 本题考查函数与方程的综合应用,函数的图象的应用,考查数形结合以及计算能力.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
4.数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn=( )
| A. | 2n-1 | B. | ${(\frac{1}{2})^{n-1}}$ | C. | ${(\frac{2}{3})^{n-1}}$ | D. | ${(\frac{3}{2})^{n-1}}$ |
14.已知函数f(x)对任意的x,y∈R都有f(x+y)=f(x)+f(y),且f(2)=4,则f(1)=( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
18.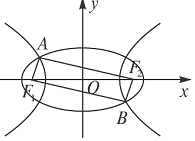 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )| A. | $y=±\sqrt{2}x$ | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{\sqrt{6}}}{2}$x |
19.已知l是双曲线$C:\frac{x^2}{4}-\frac{y^2}{2}=1$的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若PF1⊥PF2,则△PF1F2的面积为( )
| A. | 12 | B. | $3\sqrt{2}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $2\sqrt{3}$ |