题目内容
17.${∫}_{-1}^{1}$($\sqrt{1-{x}^{2}}$+|x|)dx=$\frac{π}{2}$+1.分析 利用定积分的几何意义及其计算公式,可得结论.
解答 解:${∫}_{-1}^{1}$($\sqrt{1-{x}^{2}}$+|x|)dx=${∫}_{-1}^{1}$($\sqrt{1-{x}^{2}}$)dx+${∫}_{-1}^{1}$|x|dx=$\frac{π}{2}$+2×$\frac{1}{2}{x}^{2}{|}_{0}^{1}$=$\frac{π}{2}$+1.
故答案为$\frac{π}{2}$+1.
点评 本题考查定积分的几何意义及其计算公式,比较基础.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
12.下列说法中正确的是( )
| A. | 若$\overrightarrow a•\overrightarrow b=\overrightarrow a•\overrightarrow c$,则$\vec b=\overrightarrow c$ | |
| B. | 若$\overrightarrow a•\overrightarrow b=0$,则$\vec a=\vec 0$或$\vec b=\vec 0$ | |
| C. | 若不平行的两个非零向量$\overrightarrow a,\overrightarrow b$满足$|\overrightarrow a|=|\overrightarrow b|$,则$(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-\overrightarrow b)=0$ | |
| D. | 若$\overrightarrow a$与$\overrightarrow b$平行,则$\overrightarrow a•\overrightarrow b=|\overrightarrow a|•|\overrightarrow b|$ |
7.已知四棱锥P-ABCD的底面为菱形,∠BAD=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法中错误的是( )
| A. | 异面直线PA与BC的夹角为60° | B. | 若M为AD的中点,则AD⊥平面PMB | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
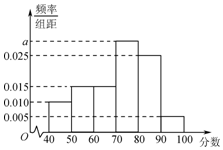 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),