��Ŀ����
11��ij�̳������н���������˿���һ��������Ʒ�ɳ齱��һ�Ƚ�500Ԫ�����Ƚ�200Ԫ�����Ƚ�10Ԫ���齱�������£��˿��ȴ�װ��2������4������ļ�����������������ٴ�װ��1������2������������������һ����������3�����У������Ǻ������һ�Ƚ�������2�����������Ƚ�����������ɫ��һ����������Ƚ����������������I����ij�˿���һ�γ齱�����ý�����ΪX����X�ķֲ��к���ѧ������
������ij��ʱ�������λ�˿Ͳμӳ齱����������һλ�ĸ��ʣ�
���� ��������֪��X�Ŀ���ȡֵΪ500��200��10��0���ֱ������Ӧ�ĸ��ʣ��ɴ�������������X�ķֲ��к��������X����ѧ������
�����ɣ���֪��һ�������еĻ���Ϊ��1-P��X=0��=$\frac{3}{5}$���ɴ����������������һ�˻ĸ��ʣ�
��� �⣺��������֪��X�Ŀ���ȡֵΪ500��200��10��0��
P��X=500��=$\frac{{C}_{2}^{2}{C}_{1}^{1}}{{C}_{6}^{2}{C}_{3}^{1}}$=$\frac{1}{45}$��
P��X=200��=$\frac{{C}_{2}^{2}{C}_{2}^{1}+{C}_{2}^{1}{C}_{4}^{1}{C}_{1}^{1}}{{C}_{6}^{2}{C}_{3}^{1}}$=$\frac{10}{45}$��
P��X=10��=$\frac{{C}_{2}^{1}{C}_{4}^{1}{C}_{2}^{1}}{{C}_{6}^{2}{C}_{3}^{1}}$=$\frac{16}{45}$��
P��X=0��=1-$\frac{1}{45}-\frac{10}{45}-\frac{16}{45}$=$\frac{18}{45}$��
���������X�ķֲ���Ϊ��
| X | 500 | 200 | 10 | 0 |
| P | $\frac{1}{45}$ | $\frac{10}{45}$ | $\frac{16}{45}$ | $\frac{18}{45}$ |
EX=$500��\frac{1}{45}+200��\frac{10}{45}+10��\frac{16}{45}$=$\frac{532}{9}$��
�����ɣ���֪��һ�������еĻ���Ϊ��
1-P��X=0��=1-$\frac{18}{45}$=$\frac{3}{5}$��
������������һ�˻ĸ���Ϊ��${C}_{3}^{1}•\frac{3}{5}•��\frac{2}{5}��^{2}+��\frac{2}{5}��^{3}$=$\frac{44}{125}$��
���� ���⿼����ʵ���������ɢ������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
19������$\frac{n}{{p}_{1}+{p}_{2}+��+{p}_{n}}$Ϊn������p1��p2������pn�ġ���������������֪����{an}����ǰn��ġ���������Ϊ$\frac{1}{5n}$����bn=$\frac{{a}_{n}}{5}$����$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+��+$\frac{1}{{b}_{10}{b}_{11}}$=��������
| A�� | $\frac{8}{17}$ | B�� | $\frac{9}{19}$ | C�� | $\frac{10}{21}$ | D�� | $\frac{11}{23}$ |
6����������z���㣨1-i��z=1+ai����ʵ��a���ڣ�������
| A�� | 0 | B�� | -1��1 | C�� | -1 | D�� | 1 |
20����ͼ������2+4+6+8+10�ij����ͼ��������ʵ��m��ȡֵ��Χ�ǣ�������
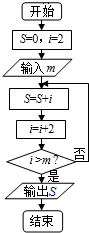

| A�� | ��10��12�� | B�� | [10��12�� | C�� | ��10��12] | D�� | [10��12] |
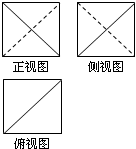 ��֪һ���ռ伸���������ͼ��ͼ��ʾ��������ͼ��Ϊ�߳�Ϊ1�������Σ������������ı����Ϊ3+$\sqrt{3}$��
��֪һ���ռ伸���������ͼ��ͼ��ʾ��������ͼ��Ϊ�߳�Ϊ1�������Σ������������ı����Ϊ3+$\sqrt{3}$��