题目内容
6.一个三棱锥的三视图如图所示,则其体积是$\frac{4}{3}$;此三棱锥的最长棱的长度为3.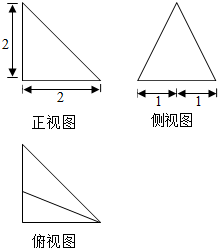
分析 根据三视图作出几何体的直观图,代入数据计算体积和棱长.
解答 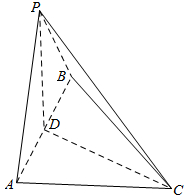 解:作出三棱锥P-ABC的直观图如图所示,由三视图可知P在底面的投影D为AB的中点,AB⊥BC,AB=AC=PD=2,
解:作出三棱锥P-ABC的直观图如图所示,由三视图可知P在底面的投影D为AB的中点,AB⊥BC,AB=AC=PD=2,
∴三棱锥的体积V=$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$.
由勾股定理可得:BC=2$\sqrt{2}$,PA=PB=$\sqrt{5}$,CD=$\sqrt{5}$,∴PC=$\sqrt{P{D}^{2}+C{D}^{2}}$=3.
∴三棱锥的棱中PC最长.
故答案为$\frac{4}{3}$,3.
点评 本题考查了棱锥的三视图和体积计算,棱锥的结构特征及几何计算.属于中档题.

练习册系列答案
相关题目
16.某三棱锥的三视图如图所示,该三棱锥的表面积是( )
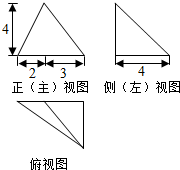

| A. | 56+12$\sqrt{5}$ | B. | 60+12$\sqrt{5}$ | C. | 30+6$\sqrt{5}$ | D. | 28+6$\sqrt{5}$ |
11.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1∥l2,l3⊥l1,l4⊥l2,则下列结论一定正确的是( )
| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
15.一个几何体的三视图如图所示,则该几何体的表面积是( )
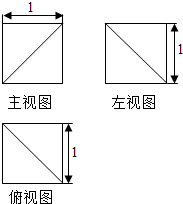

| A. | $\frac{{9+\sqrt{3}}}{2}$ | B. | 5 | C. | $\frac{{18+\sqrt{3}}}{4}$ | D. | $4+\sqrt{2}$ |
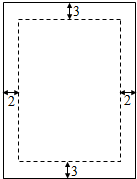 如图,有一矩形相框,放置照片区域的上、下方要各留3cm空白,左、右两侧要各留2cm的空白.
如图,有一矩形相框,放置照片区域的上、下方要各留3cm空白,左、右两侧要各留2cm的空白.