题目内容
1．如图，已知长方形ABCD中，AD=$\frac{1}{2}$AB=a，M为CD的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM，点O是线段AM的中点．（1）求证：AD⊥BM；
（2）若三棱锥C-BMD的高为2，求a的值和△CDM的面积．
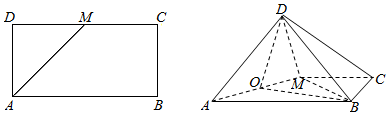
分析 （1）根据线面垂直的性质即可证明AD⊥BM；
（2）取AM的中点O，连接DO，则DO⊥AM，可得DO⊥平面ADM，即可求a的值和△CDM的面积．
解答 （1）证明：∵矩形ABCD中，AB=2a，AD=a，M为DC的中点，∴AM=BM=$\sqrt{2}$a，
∴AM2+BM2=AB2，∴AM⊥BM．
再由平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，∴BM⊥平面ADM，
结合AD?平面ADM，可得AD⊥BM．
（2）解：取AM的中点O，连接DO，则DO⊥AM，
由平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，∴DO⊥平面ADM，
∴DO=2，∴a=2$\sqrt{2}$．
∵DO=2，O到直线CM的距离为$\sqrt{2}$，
∴D到直线CM的距离为$\sqrt{4+2}$=$\sqrt{6}$，
∴△CDM的面积S=$\frac{1}{2}×2\sqrt{2}×\sqrt{6}$=2$\sqrt{3}$．
点评 本题考查平面与平面垂直的性质，考查线面垂直，考查学生的计算能力，属于中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
16．设a=0.5${\;}^{\frac{1}{2}}}$，b=0.9${\;}^{\frac{1}{4}}}$，c=log50.3，则a，b，c的大小关系是（ ）
| A． | a＞c＞b | B． | c＞a＞b | C． | a＞b＞c | D． | b＞a＞c |
6．a，b满足2a+b=2，则直线ax+2y+b=0必过定点（ ）
| A． | （0，2-2a） | B． | （1，2） | C． | （2，2） | D． | （2，-1） |
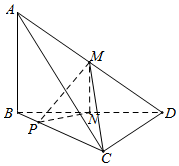在三棱锥A-BCD中，AB⊥平面BCD，DB=DC=4，∠BDC=90°，P在线段BC上，CP=3PB，M，N分别为AD，BD的中点．
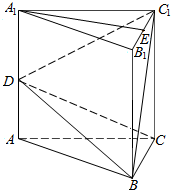三棱柱ABC-A1B1C1中，AA1⊥面ABC，BC⊥AC，AC=BC=1，AA1=2，点D、E分别为AA1、B1C1的中点．