题目内容
15．设O为原点，点M在圆C：（x-3）2+（y-4）2=1上运动，则|OM|的最大值为6．分析 先求出圆心和半径r，再求得|CO|=5，则|OM|的最大值为|CO|+r．
解答 解：圆C：（x-3）2+（y-4）2=1，表示以C（3，4）为圆心，半径r等于1的圆．
由于|CO|=5，∴|OM|的最大值为|CO|+r=6，
故答案为：6
点评 本题主要考查圆的标准方程，点与圆的位置关系，属于中档题．
练习册系列答案
相关题目
5．函数y=log${\;}_{\frac{1}{3}}$（x2-ax+3）在[1，2]上恒为正数，则a的取值范围是（ ）
| A． | 2$\sqrt{2}$＜a＜2$\sqrt{3}$ | B． | 2$\sqrt{2}$＜a＜$\frac{7}{2}$ | C． | 3＜a＜$\frac{7}{2}$ | D． | 3＜a＜2$\sqrt{3}$ |
6．a，b满足2a+b=2，则直线ax+2y+b=0必过定点（ ）
| A． | （0，2-2a） | B． | （1，2） | C． | （2，2） | D． | （2，-1） |
3．函数f（x）=x2-x-1的零点有（ ）
| A． | 2个 | B． | 1个 | C． | 0个 | D． | 都有可能 |
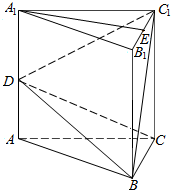三棱柱ABC-A1B1C1中，AA1⊥面ABC，BC⊥AC，AC=BC=1，AA1=2，点D、E分别为AA1、B1C1的中点．