题目内容
20.已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )| A. | ?x0∈R,f(x0)=0 | |
| B. | 若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减 | |
| C. | 函数f(x)的图象是中心对称图形 | |
| D. | 若x0是f(x)的极值点,则f′(x0)=0 |
分析 求函数的导数,根据函数单调性,极值和导数的关系进行判断即可.
解答 解:A.当x→+∞时,f(x)→+∞,当x→-∞时,f(x)→-∞,即?x0∈R,f(x0)=0,故A正确,
B.(1)当△=4a2-12b>0时,f′(x)=0有两解,不妨设为x1<x2,列表如下
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
即若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减,错误,故B不正确.
C.∵f(-$\frac{2a}{3}$-x)+f(x)=[${(-\frac{2a}{3}-x)}^{3}$+a${(-\frac{2a}{3}-x)}^{2}$+b(-$\frac{2a}{3}$-x)+c]+(x3+ax2+bx+c)=$\frac{{4a}^{3}}{9}$-$\frac{2ab}{3}$+2c,
f(-$\frac{a}{3}$)=$\frac{{2a}^{3}}{9}$-$\frac{ab}{3}$+c,
∴f(-$\frac{2a}{3}$-x)+f(x)=2f(-$\frac{a}{3}$),
∴f(x)关于点P(-$\frac{a}{3}$,f(-$\frac{a}{3}$))成中心对称,∴故函数y=f(x)的图象一定是中心对称图形,故C正确,
D.根据函数极值点的定义和性质值,若若x0是f(x)的极值点,则f′(x0)=0,故D正确,
故选:B.
点评 本题考查命题的真假判断与应用,着重考查导函数与极值的应用,要求熟练掌握三次函数的图象和性质,属于中档题

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
5.函数y=log${\;}_{\frac{1}{3}}$(x2-ax+3)在[1,2]上恒为正数,则a的取值范围是( )
| A. | 2$\sqrt{2}$<a<2$\sqrt{3}$ | B. | 2$\sqrt{2}$<a<$\frac{7}{2}$ | C. | 3<a<$\frac{7}{2}$ | D. | 3<a<2$\sqrt{3}$ |
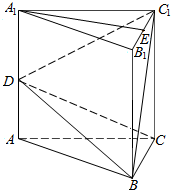 三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.
三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=1,AA1=2,点D、E分别为AA1、B1C1的中点.