题目内容
11．
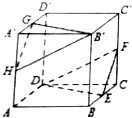在正方体ABCD-A′B′C′D′中，E、F、G、H分别为BC、CC′、A′D′、AA′的中点．求证：平面DEF∥平面B'GH．
分析 利用线面平行，证明平面与平面平行．
解答 
证明：连BC'、AD'，作AD中点M，连BM，则
∵E、F、G、H分别为BC、CC′、A′D′、AA′的中点，
∴EF∥BC'∥AD'∥GH，DE∥BM∥B'G，
∵EF?面B'GH，DE?面B'GH，GH?面B'GH，B′G?面B'GH，
∴EF∥面B'GH，DE∥面B'GH，
∵EF∩DE=E，
∴面DEF∥面B'GH．
点评 本题考查线面平行、面面平行，关键是证明线面平行．
练习册系列答案
相关题目
2．已知函数f（x）=a-x+xex，若存在x0＞-1，使得f（x0）≤0，则实数a的取值范围为（ ）
| A． | [0，+∞） | B． | （-∞，0] | C． | [1，+∞） | D． | （-∞，1] |
16．已知函f（x）=$\left\{\begin{array}{l}{2cos\frac{πx}{3}（x≤2000）}\\{{2}^{x-2008}（x＞2000）}\end{array}\right.$ 则f[f（2015）]等于（ ）
| A． | $\sqrt{3}$ | B． | -$\sqrt{3}$ | C． | 1 | D． | -1 |
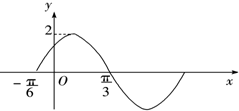函数f1（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的一段图象如图所示．