题目内容
16.已知函f(x)=$\left\{\begin{array}{l}{2cos\frac{πx}{3}(x≤2000)}\\{{2}^{x-2008}(x>2000)}\end{array}\right.$ 则f[f(2015)]等于( )| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
分析 由分段函数f(x),先求得f(2015)=128,再求f(128),运用三角函数的诱导公式和特殊角的余弦函数值,即可得到所求值.
解答 解:函数f(x)=$\left\{\begin{array}{l}{2cos\frac{πx}{3}(x≤2000)}\\{{2}^{x-2008}(x>2000)}\end{array}\right.$,
可得f(2015)=22015-2008=27=128,
f[f(2015)]=f(128)=2cos$\frac{128π}{3}$=2cos(42π+$\frac{2π}{3}$)
=2cos$\frac{2π}{3}$=2×(-$\frac{1}{2}$)=-1.
故选:D.
点评 本题考查分段函数的应用:求函数值,注意运用各段的解析式,考查指数和三角函数的化简运算,属于基础题.

练习册系列答案
相关题目
2.$\int_{\frac{π}{2}}^π{(sinx+cosx)}dx$的值是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | 2 | D. | 4 |
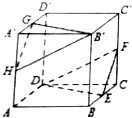 在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.
在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.