题目内容
3.求证:函数f(x)=x+$\frac{1}{\sqrt{x}}$在区间(1,+∞)上是单调递增函数.分析 设任意的x1>x2>1,然后作差,通分,用上平方差公式,从而提取公因式,这样便可证明f(x1)>f(x2),从而得出证明的结论.
解答 证明:设x1>x2>1,则:
$f({x}_{1})-f({x}_{2})={x}_{1}+\frac{1}{\sqrt{{x}_{1}}}-{x}_{2}-\frac{1}{\sqrt{{x}_{2}}}$
=$({x}_{1}-{x}_{2})-\frac{\sqrt{{x}_{1}}-\sqrt{{x}_{2}}}{\sqrt{{x}_{1}}\sqrt{{x}_{2}}}$
=$(\sqrt{{x}_{1}}-\sqrt{{x}_{2}})(\sqrt{{x}_{1}}+\sqrt{{x}_{2}}-\frac{1}{\sqrt{{x}_{1}}\sqrt{{x}_{2}}})$;
∵x1>x2>1;
∴$\sqrt{{x}_{1}}>\sqrt{{x}_{2}}>1$;
∴$\sqrt{{x}_{1}}-\sqrt{{x}_{2}}>0$,$\frac{1}{\sqrt{{x}_{1}}\sqrt{{x}_{2}}}<1$,$\sqrt{{x}_{1}}+\sqrt{{x}_{2}}-\frac{1}{\sqrt{{x}_{1}}\sqrt{{x}_{2}}}>0$;
∴$(\sqrt{{x}_{1}}-\sqrt{{x}_{2}})(\sqrt{{x}_{1}}+\sqrt{{x}_{2}}-\frac{1}{\sqrt{{x}_{1}}\sqrt{{x}_{2}}})>0$;
∴f(x1)>f(x2);
∴函数f(x)在区间(1,+∞)上是单调递增函数.
点评 考查增函数的定义,以及根据增函数定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1),f(x2)的大小关系,平方差公式的运用,作差后是分式的一般要通分.

 名校课堂系列答案
名校课堂系列答案| A. | ac=0 | B. | ac<0 | C. | ac>0 | D. | a+c>0 | ||||
| E. | a+c<0 |
| A. | 4 | B. | 8 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
| A. | (1,3) | B. | (-1,3) | C. | (3,-1) | D. | (-3,-1) |
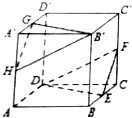 在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.
在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.