题目内容
17.下面四个函数:(1)y=1-x;(2)y=2x-1;(3)y=x2-1;(4)y=$\frac{5}{x}$,其中定义域与值域相同的函数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别求出四个函数的定义域和值域,比较得答案.
解答 解:(1)y=1-x的定义域为R,值域为R;
(2)y=2x-1的定义域为R,值域为R;
(3)y=x2-1的定义域为R,值域为[-1,+∞);
(4)y=$\frac{5}{x}$的定义域为(-∞,0)∪(0,+∞),值域为(-∞,0)∪(0,+∞).
∴其中定义域与值域相同的函数有3个.
故选:C.
点评 本题考查基本初等函数的定义域和值域的求法,是基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
8.已知等比数列{an}各项都为正数,且满足a2=2,a6=6,a4=( )
| A. | 4 | B. | 8 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
5.已知{an}为等差数列,{bn}为正项等比数列,公比q≠1,若a1=b1,a13=b13,则( )
| A. | a7=b7 | B. | a7>b7 | C. | a7<b7 | D. | a7>b7或a7<b7 |
2.$\int_{\frac{π}{2}}^π{(sinx+cosx)}dx$的值是( )
| A. | 0 | B. | $\frac{π}{4}$ | C. | 2 | D. | 4 |
9.两直线x-2y+7=0和2x+y-1=0的交点坐标为( )
| A. | (1,3) | B. | (-1,3) | C. | (3,-1) | D. | (-3,-1) |
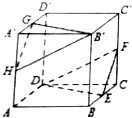 在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.
在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.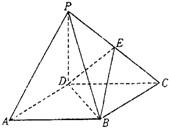 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.