题目内容
1.已知函数f(x)=x2+x,x1,x2∈R,则下列不等式中一定成立的不等式的序号为①①f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;
②f($\frac{{x}_{1}+{x}_{2}}{2}$)<$\frac{f({x}_{1})+f({x}_{2})}{2}$;
③f($\frac{{x}_{1}+{x}_{2}}{2}$)≥$\frac{f({x}_{1})+f({x}_{2})}{2}$;
④f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$.
分析 作差,判断2$f(\frac{{x}_{1}{+x}_{2}}{2})$-f(x1)-f(x2)的符号即可.
解答 解:2$f(\frac{{x}_{1}{+x}_{2}}{2})$-f(x1)-f(x2)
=2•${(\frac{{x}_{1}{+x}_{2}}{2})}^{2}$+x1+x2-${{x}_{1}}^{2}$-x1-${{x}_{2}}^{2}$-x2
=-$\frac{1}{2}$${{x}_{1}}^{2}$+x1x2-$\frac{1}{2}$${{x}_{2}}^{2}$
=-$\frac{1}{2}$${{(x}_{1}{-x}_{2})}^{2}$≤0,
∴f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;
故答案为:①.
点评 本题考查了函数值的大小比较,考查二次函数的性质,是一道基础题.

练习册系列答案
相关题目
11.已知sin($\frac{π}{2}$-α)=$\frac{5}{13}$,且α是第四象限的角,则tan(2π-α)=( )
| A. | -$\frac{12}{5}$ | B. | $\frac{12}{5}$ | C. | ±$\frac{12}{5}$ | D. | ±$\frac{5}{12}$ |
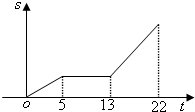 某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法:
某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法: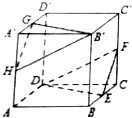 在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.
在正方体ABCD-A′B′C′D′中,E、F、G、H分别为BC、CC′、A′D′、AA′的中点.求证:平面DEF∥平面B'GH.