题目内容

（x3+
1
x2
）10的展开式中的常数项是（　　）
A、
C
5
10
B、
C
6
10
C、
C
9
10
D、
C
10
10
考点：二项式系数的性质
专题：二项式定理
分析：在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．
解答： 解：（x3+
1
x2
）10的展开式的通项公式为Tr+1=
C
r
10
•x30-5r，
令30-5r=0，求得r=6，
故展开式中的常数项是
C
6
10
，
故选：B．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于中档题．
练习册系列答案
相关题目
下列命题：
①若
a
•
b
=
b
•
c
，则
a
=
c
；
②若
a
与
b
是共线向量，
b
与
c
是共线向量，则
a
与
c
是共线向量；
③若|
a
+
b
|=|
a
-
b
|，则
a
•
b
=0；
④若
a
，
b
均为非零向量，且方向相反，则|
a
-
b
|=|
a
|-|
b
|．
其中真命题的个数是
 
．
一个长方体被一平面截去一部分所得几何体的三视图如图，则该几何体的体积是（　　）
A、1440B、1200
C、960D、720
已知α，β是任意角，则“sinα=cosα”是“cos（α+β）=sin（α-β）”的（　　）
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
tan（-
41π
3
）等于（　　）
A、
3
B、-
3
3
C、-
3
D、
3
3
已知0＜m1＜2＜m2，且logam1=m1-1，logam2=m2-1，则实数a的取值范围是（　　）
A、2＜a＜3
B、0＜a＜1
C、1＜a＜2
D、3＜a＜4
已知函数f1（x）=sinx+cosx，记f2（x）=f′1（x），f3（x）=f′2（x），…，fn（x）=f′n-1（x）（n∈N*，n≥2），则f1（
π
2
）+f2（
π
2
）+…+f2014（
π
2
）的值是（　　）
A、-1B、0C、1D、2
已知向量
a
=（1，2），
b
=（x，1），
u
=
a
+2
b
，
v
=2
a
-
b
，且
u
∥
v
，求x的值．
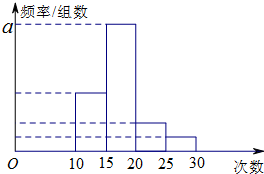对某校高三学生一个月内参加体育活动的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加体育活动的次数．根据此数据做出了频数与频率的统计表和频率分布直方图如下：
分组频数频率
[10，15）100.25
[15，20）24n
[20，25）mp
[25，30]20.05
合计M1
（Ⅰ）求出表中M，p及图中a的值；
（Ⅱ）若该校高三学生有240人，试估计该校高三学生在一个月内参加体育活动的次数在区间[10，15）内的人数；
（Ⅲ）在所取的样本中，从参加体育活动的次数不少于20次的学生中任取4人，记此4人中参加体育活动不少于25次的人数为ξ，求随机变量ξ的分布列和数学期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网