题目内容
设m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列为真命题的是( )
| A、若α⊥β,m⊥α,则m∥β |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若m⊥α,n∥m,则n⊥α |
| D、若m∥α,n∥α,则m∥n |
考点:平面与平面之间的位置关系,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用线面平行以及面面平行的判定定理以及性质定理对四个选项分别分析解答.A:漏掉了m?β.B:可以举出墙角的例子.C根据线线垂直的判定可得结论是正确的.D:漏掉了m与n相交、异面的情况.
解答:
解:对于A:直线m也可以在平面β内.
对于B:α与β也可以相交.可以举出墙角的例子.
对于C:根据线面垂直的判定和性质可得结论是正确的.
对于D:m与n可能平行也可能相交也可能异面.
故选C.
对于B:α与β也可以相交.可以举出墙角的例子.
对于C:根据线面垂直的判定和性质可得结论是正确的.
对于D:m与n可能平行也可能相交也可能异面.
故选C.
点评:本题考查了空间线面关系、面面关系以及线线关系;解决此类问题的关键是熟练掌握空间中线面之间的相互平行、相互垂直的判定定理与性质定理,熟记相关的结论.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
加工一种零件需要三道工序,其中只会第一道工序的有4人,只会第二道工序的有2人,只会第三道工序的有3人,现在从每道工序中各选一人加工这种零件,共有( )种不同的选派方法.
| A、9 | B、12 | C、24 | D、30 |
若函数f(x)满足:存在非零常数a,使f(x)=-f(2a-x),则称f(x)为“准奇函数”,下列函数中是“准奇函数”的是( )
| A、f(x)=x2 |
| B、f(x)=(x-1)3 |
| C、f(x)=ex-1 |
| D、f(x)=x3 |
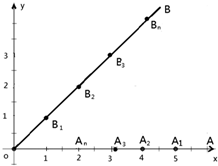 平面直角坐标系中,O为原点,射线OA与x轴正半轴重合,射线OB是第一象限角平分线.在OA上有点列A1,A2,A3,…,An,…,在OB上有点列B1,B2,B3,…,Bn,…已知
平面直角坐标系中,O为原点,射线OA与x轴正半轴重合,射线OB是第一象限角平分线.在OA上有点列A1,A2,A3,…,An,…,在OB上有点列B1,B2,B3,…,Bn,…已知