题目内容
函数f(x)=x2+3x+2在区间[-5,5]上的最大值,最小值分别为 .
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:对函数f(x)进行配方,通过配方后的解析式即可看出x取何值时,f(x)取到最大值,最小值.
解答:
解:f(x)=x2+3x+2=(x+
)2-
;
∴x=-
时,f(x)取到最小值-
;
x=5时,f(x)在[-5,5]上取到最大值42.
故答案为:42,-
.
| 3 |
| 2 |
| 1 |
| 4 |
∴x=-
| 3 |
| 2 |
| 1 |
| 4 |
x=5时,f(x)在[-5,5]上取到最大值42.
故答案为:42,-
| 1 |
| 4 |
点评:考查通过配方求二次函数在闭区间上的最值的方法.

练习册系列答案
相关题目
下列结论正确的是 ( )
| A、20.2>20.1 |
| B、log34<log32 |
| C、0.3-1>0.2-1 |
| D、0.43<0.45 |
已知长方体的对角线长为4,过同一顶点的两条棱与此对角线成角均为60°,则长方体的体积是( )
A、16
| ||
B、8
| ||
C、8
| ||
D、4
|
有5条线段长度分别为1,3,5,7,9,从中任意取出3条,则所取3条线段可构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
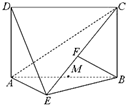 如图,四边形ABCD为矩形,∠AEB=
如图,四边形ABCD为矩形,∠AEB=