题目内容
设函数f(x)=xlnx(x>0)
(1)求函数f(x)的最小值;
(2)设F(x)=ax2+f′(x)(a∈R),讨论函数F(x)的单调性;
(3)当x>0时,证明:ex>f′(x)+1.
(1)求函数f(x)的最小值;
(2)设F(x)=ax2+f′(x)(a∈R),讨论函数F(x)的单调性;
(3)当x>0时,证明:ex>f′(x)+1.
考点:利用导数研究函数的单调性,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(1)求得函数的定义域,求导函数,确定函数的单调性,即可求得函数f(x)的最小值.
(2)分类讨论,利用导数的正负,即可得到函数F(x)的单调性.
(3)证明ex-f′(x)-1>0,在x>0时恒成立,即可得到结论.
(2)分类讨论,利用导数的正负,即可得到函数F(x)的单调性.
(3)证明ex-f′(x)-1>0,在x>0时恒成立,即可得到结论.
解答:
解:(1)∵函数f(x)=xlnx的定义域为(0,+∞),且f′(x)=1+lnx
令f′(x)=1+lnx=0,可得x=
,
∴0<x<
时,f′(x)<0,x>
时,f′(x)>0
∴x=
时,函数取得极小值,也是函数的最小值
∴f(x)min=f(
)=
•ln
=-
.
(2)F(x)=ax2+lnx+1(x>0),
F′(x)=
(x>0).
①当a≥0时,恒有F′(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,令F′(x)>0,得2ax2+1>0,解得0<x<
;
令F′(x)<0,得2ax2+1<0,解得x>
.
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在(0,
)上单调递增,在(
,+∞)上单调递减.
证明:(3)令h(x)=ex-f′(x)-1=ex-lnx-2,x>0,
则h′(x)=ex-
,令h′(a)=ea-
=0,
则ea=
,a=e-a,
则0<x<a时,h′(x)<0,x>a时,h′(x)>0
∴x=a时,函数取得极小值,也是函数的最小值ea-lna-2=
+a-2>0,
故ex-lnx-2>0在x>0时恒成立,
故当x>0时,证明:ex>f′(x)+1.
令f′(x)=1+lnx=0,可得x=
| 1 |
| e |
∴0<x<
| 1 |
| e |
| 1 |
| e |
∴x=
| 1 |
| e |
∴f(x)min=f(
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
(2)F(x)=ax2+lnx+1(x>0),
F′(x)=
| 2ax2+1 |
| x |
①当a≥0时,恒有F′(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,令F′(x)>0,得2ax2+1>0,解得0<x<
-
|
令F′(x)<0,得2ax2+1<0,解得x>
-
|
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在(0,
-
|
-
|
证明:(3)令h(x)=ex-f′(x)-1=ex-lnx-2,x>0,
则h′(x)=ex-
| 1 |
| x |
| 1 |
| a |
则ea=
| 1 |
| a |
则0<x<a时,h′(x)<0,x>a时,h′(x)>0
∴x=a时,函数取得极小值,也是函数的最小值ea-lna-2=
| 1 |
| a |
故ex-lnx-2>0在x>0时恒成立,
故当x>0时,证明:ex>f′(x)+1.
点评:本题考查导数知识的运用,考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设f(x)是定义在(-∞,+∞)上可导函数且满足xf'(x)+f(x)>0对任意的正数a,b,若a>b则下列不等式恒成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
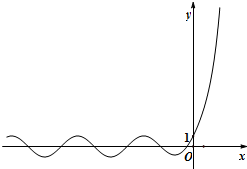 已知函数:y=x2,y=log2x,y=2x,y=sinx,y=cosx,y=tanx.从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=
已知函数:y=x2,y=log2x,y=2x,y=sinx,y=cosx,y=tanx.从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=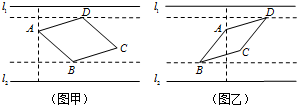 如图,某兴趣小组测得菱形养殖区ABCD的固定投食点A到两条平行河岸线l1、l2的距离分别为4米、8米,河岸线l1与该养殖区的最近点D的距离为1米,l2与该养殖区的最近点B的距离为2米.
如图,某兴趣小组测得菱形养殖区ABCD的固定投食点A到两条平行河岸线l1、l2的距离分别为4米、8米,河岸线l1与该养殖区的最近点D的距离为1米,l2与该养殖区的最近点B的距离为2米.