题目内容
在锐角△ABC中，角A，B，C的对边分别为a，b，c且sin2A-cosA=0．
（1）求角A的大小；
（2）若b=
，sinB=
sinC，求a．
（1）求角A的大小；
（2）若b=
| 3 |
| 3 |
考点：正弦定理
专题：解三角形
分析：（1）已知等式利用二倍角的正弦函数公式化简，整理求出sinA的值，即可确定出A的度数；
（2）已知等式利用正弦定理化简，把b的值代入求出c的值，利用余弦定理列出关系，将b，c，cosA的值代入即可求出a的值．
（2）已知等式利用正弦定理化简，把b的值代入求出c的值，利用余弦定理列出关系，将b，c，cosA的值代入即可求出a的值．
解答：
解：（1）由sin2A-cosA=0，得2sinAcosA-cosA=0，
即cosA（2sinA-1）=0得cosA=0或sinA=
，
∵△ABC为锐角三角形，
∴sinA=
，
则A=
；
（2）把sinB=
sinC，由正弦定理得b=
c，
∵b=
，∴c=1，
由余弦定理得：a2=b2+c2-2bccosA=3+1-2×
×1×
=1，
解得：a=1．
即cosA（2sinA-1）=0得cosA=0或sinA=
| 1 |
| 2 |
∵△ABC为锐角三角形，
∴sinA=
| 1 |
| 2 |
则A=
| π |
| 6 |
（2）把sinB=
| 3 |
| 3 |
∵b=
| 3 |
由余弦定理得：a2=b2+c2-2bccosA=3+1-2×
| 3 |
| ||
| 2 |
解得：a=1．
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
若等比数列{an}的前3项的和S3=14，且a2=4，公比大于1，则a7=（ ）
| A、182 | B、46 |
| C、64 | D、128 |
已知a的第四象限的角，且sin（
+α）=
，则tanα=（ ）
| π |
| 2 |
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
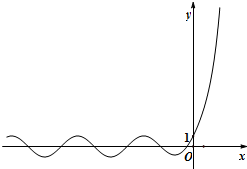已知函数：y=x2，y=log2x，y=2x，y=sinx，y=cosx，y=tanx．从中选出两个函数记为f（x）和g（x），若F（x）=f（x）+g（x）的图象如图所示，则F（x）=